Question

4 $2mg = N_1 + T_1 = N_2 + T_2$ - ①

$3T_2 = N_1 + 4N_2 + 2mg$ - ②

$3T_1 + N_2 = mg + 2N_1$ - ③

$T_1 + T_2 = N_1 + N_2 + mg$ - ④

$T_1 + T_2 = \frac{5mg}{2}$ - ⑤

$N_1 + N_2 = \frac{3mg}{2}$ - ⑥

Answer 1

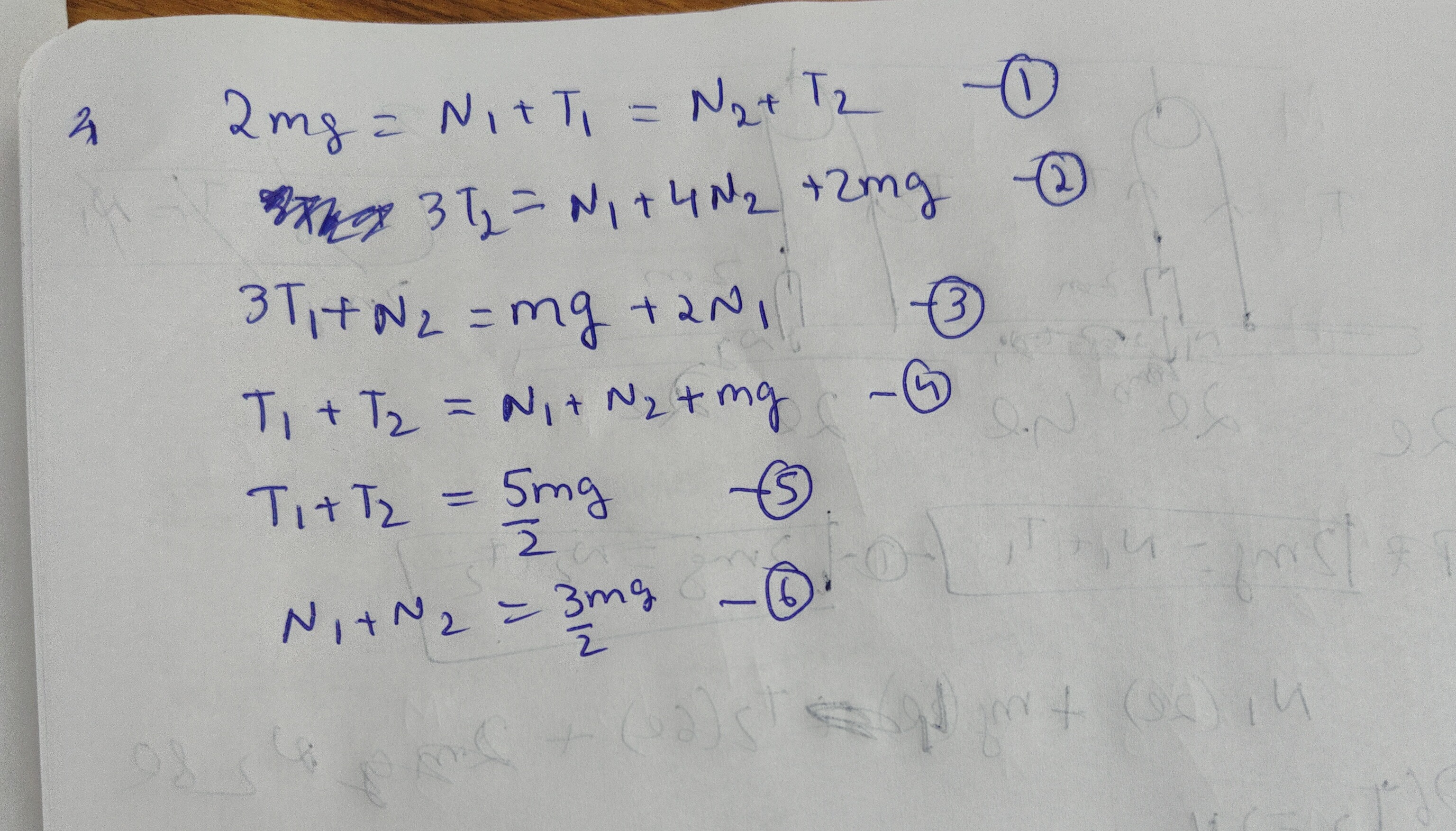
N_1 = \frac{13mg}{12}, N_2 = \frac{5mg}{12}, T_1 = \frac{11mg}{12}, T_2 = \frac{19mg}{12}

Answer 2

The problem presents a system of six linear equations involving four variables ($N_1, N_2, T_1, T_2$) and a constant $mg$. The objective is to find the values of these variables in terms of $mg$.

First, let's clarify the interpretation of the first equation. The formatting "4 $2mg = N_1 + T_1 = N_2 + T_2$ - ①" is ambiguous. We will assume the most common interpretation in physics problems where the numerical prefix '4' is a typo for the equation number, and the equation itself is: $2mg = N_1 + T_1 = N_2 + T_2$

So, the system of equations is:

1. $N_1 + T_1 = 2mg$
2. $N_2 + T_2 = 2mg$
3. $3T_2 = N_1 + 4N_2 + 2mg$
4. $3T_1 + N_2 = mg + 2N_1$
5. $T_1 + T_2 = \frac{5mg}{2}$
6. $N_1 + N_2 = \frac{3mg}{2}$

Let's check the consistency of equations (1), (2), (5), and (6). Summing equations (1) and (2): $(N_1 + T_1) + (N_2 + T_2) = 2mg + 2mg$ $(N_1 + N_2) + (T_1 + T_2) = 4mg$

Now, substitute equations (5) and (6) into this sum: $(\frac{3mg}{2}) + (\frac{5mg}{2}) = 4mg$ $\frac{8mg}{2} = 4mg$ $4mg = 4mg$ This confirms that equations (1), (2), (5), and (6) are consistent with each other. Also, equation (4) $T_1 + T_2 = N_1 + N_2 + mg$ is consistent with (5) and (6) because $\frac{5mg}{2} = \frac{3mg}{2} + mg$ is true. Thus, equation (4) is redundant if (5) and (6) are given.

Now we have four independent equations (1, 2, 3, 5, 6, with 4 being redundant) and four variables. Let's solve for $N_1, N_2, T_1, T_2$.

From (6), $N_1 = \frac{3mg}{2} - N_2$. From (5), $T_1 = \frac{5mg}{2} - T_2$.

Substitute these into equation (1): $(\frac{3mg}{2} - N_2) + (\frac{5mg}{2} - T_2) = 2mg$ $\frac{8mg}{2} - (N_2 + T_2) = 2mg$ $4mg - (N_2 + T_2) = 2mg$ $N_2 + T_2 = 2mg$ This is identical to equation (2), so it doesn't give new information about $N_2$ and $T_2$ alone.

Let's use equations (2) and (3) to find $N_2$ and $T_2$. From (2): $T_2 = 2mg - N_2$. Substitute this into (3): $3(2mg - N_2) = N_1 + 4N_2 + 2mg$ $6mg - 3N_2 = N_1 + 4N_2 + 2mg$ $4mg = N_1 + 7N_2$

Now substitute $N_1 = \frac{3mg}{2} - N_2$ into this equation: $4mg = (\frac{3mg}{2} - N_2) + 7N_2$ $4mg = \frac{3mg}{2} + 6N_2$ $4mg - \frac{3mg}{2} = 6N_2$ $\frac{8mg - 3mg}{2} = 6N_2$ $\frac{5mg}{2} = 6N_2$ $N_2 = \frac{5mg}{12}$

Now find $T_2$ using $T_2 = 2mg - N_2$: $T_2 = 2mg - \frac{5mg}{12} = \frac{24mg - 5mg}{12} = \frac{19mg}{12}$

Now find $N_1$ using $N_1 = \frac{3mg}{2} - N_2$: $N_1 = \frac{3mg}{2} - \frac{5mg}{12} = \frac{18mg - 5mg}{12} = \frac{13mg}{12}$

Finally, find $T_1$ using $T_1 = 2mg - N_1$: $T_1 = 2mg - \frac{13mg}{12} = \frac{24mg - 13mg}{12} = \frac{11mg}{12}$

Let's verify these values by substituting them into equation (4) $3T_1 + N_2 = mg + 2N_1$: LHS: $3T_1 + N_2 = 3(\frac{11mg}{12}) + \frac{5mg}{12} = \frac{33mg}{12} + \frac{5mg}{12} = \frac{38mg}{12} = \frac{19mg}{6}$ RHS: $mg + 2N_1 = mg + 2(\frac{13mg}{12}) = mg + \frac{26mg}{12} = mg + \frac{13mg}{6} = \frac{6mg + 13mg}{6} = \frac{19mg}{6}$ LHS = RHS. All equations are satisfied.

The values are: $N_1 = \frac{13mg}{12}$ $N_2 = \frac{5mg}{12}$ $T_1 = \frac{11mg}{12}$ $T_2 = \frac{19mg}{12}$

The question asks to solve the given equations. The solution is the set of values for $N_1, N_2, T_1, T_2$.

The final answer is $\boxed{N_1 = \frac{13mg}{12}, N_2 = \frac{5mg}{12}, T_1 = \frac{11mg}{12}, T_2 = \frac{19mg}{12}}$

Explanation of the solution: The given system of six linear equations with four variables ($N_1, N_2, T_1, T_2$) was solved. First, the ambiguity in equation (1) was resolved by interpreting "4 $2mg$" as $2mg$, assuming '4' is a typo for the equation number. The consistency of the system was checked by summing equations (1) and (2) and comparing with (5) and (6), which confirmed consistency. It was also noted that equation (4) is redundant as it can be derived from (5) and (6). The system was then solved using substitution. Expressions for $N_1$ and $T_1$ in terms of $N_2$ and $T_2$ were derived from (5) and (6). These were substituted into other equations to reduce the number of variables. Ultimately, $N_2$ was found using equations (2), (3), and (6). Once $N_2$ was known, $T_2$, $N_1$, and $T_1$ were calculated using the derived relations. All values were verified by substituting them back into one of the original equations.