Question

100 ml of 0.1 M solution of AB (d = 1.5 gm/ml) is mixed with 100 ml of 0.2 M solution of CB₂ (d = 2.5 gm/ml). Calculate the molarity of $B^-$ in final solution if the density of final solution is 4 gm/ml. Assuming AB and CB₂ are non reacting & dissociates completely into $A^+, B^-, C^{+2}$.

Answer 1

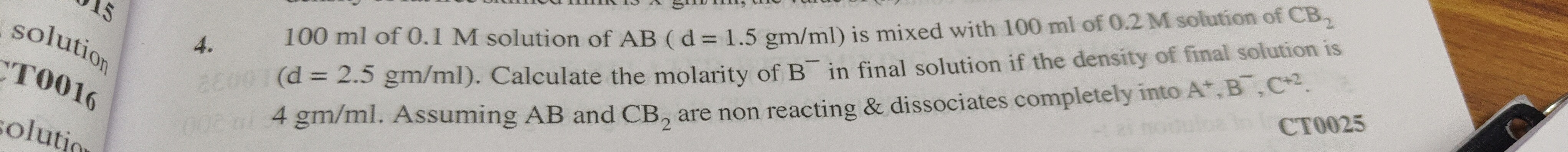
0.5 M

Answer 2

The problem requires calculating the molarity of B⁻ ions in a final solution formed by mixing two initial solutions, AB and CB₂.

1. Calculate moles of B⁻ from each solution:

• For AB solution:

  • Volume (V₁): 100 ml = 0.1 L
  • Molarity (M₁): 0.1 M
  • Moles of AB (n_AB) = M₁ × V₁ = 0.1 mol/L × 0.1 L = 0.01 mol
  • Since AB dissociates completely ($AB \rightarrow A^+ + B^-$), moles of B⁻ from AB = 0.01 mol.

• For CB₂ solution:

  • Volume (V₂): 100 ml = 0.1 L
  • Molarity (M₂): 0.2 M
  • Moles of CB₂ (n_CB₂) = M₂ × V₂ = 0.2 mol/L × 0.1 L = 0.02 mol
  • Since CB₂ dissociates completely ($CB_2 \rightarrow C^{+2} + 2B^-$), moles of B⁻ from CB₂ = 2 × n_CB₂ = 2 × 0.02 mol = 0.04 mol.

2. Calculate total moles of B⁻ in the final solution:

• Total moles of B⁻ (n_B⁻_total) = Moles of B⁻ from AB + Moles of B⁻ from CB₂
• n_B⁻_total = 0.01 mol + 0.04 mol = 0.05 mol

3. Calculate the mass of each initial solution:

• Mass of AB solution (m₁) = Volume₁ × Density₁ = 100 ml × 1.5 gm/ml = 150 gm
• Mass of CB₂ solution (m₂) = Volume₂ × Density₂ = 100 ml × 2.5 gm/ml = 250 gm

4. Calculate the total mass of the final solution:

• Total mass (m_final) = m₁ + m₂ = 150 gm + 250 gm = 400 gm

5. Calculate the total volume of the final solution:

• Density of final solution (d_final) = 4 gm/ml
• Total volume (V_final) = m_final / d_final = 400 gm / 4 gm/ml = 100 ml
• Convert volume to Liters: V_final = 100 ml = 0.1 L

6. Calculate the molarity of B⁻ in the final solution:

• Molarity of B⁻ (M_B⁻) = n_B⁻_total / V_final
• M_B⁻ = 0.05 mol / 0.1 L = 0.5 M

The molarity of B⁻ in the final solution is 0.5 M.

Explanation of the solution:

1. Calculate moles of B⁻ from AB ($0.1 \text{ M} \times 0.1 \text{ L} = 0.01 \text{ mol}$).
2. Calculate moles of B⁻ from CB₂ ($0.2 \text{ M} \times 0.1 \text{ L} \times 2 = 0.04 \text{ mol}$).
3. Sum to find total moles of B⁻ ($0.01 + 0.04 = 0.05 \text{ mol}$).
4. Calculate mass of AB solution ($100 \text{ ml} \times 1.5 \text{ gm/ml} = 150 \text{ gm}$).
5. Calculate mass of CB₂ solution ($100 \text{ ml} \times 2.5 \text{ gm/ml} = 250 \text{ gm}$).
6. Sum to find total mass of final solution ($150 + 250 = 400 \text{ gm}$).
7. Calculate total volume of final solution ($400 \text{ gm} / 4 \text{ gm/ml} = 100 \text{ ml} = 0.1 \text{ L}$).
8. Divide total moles of B⁻ by total volume to find molarity ($0.05 \text{ mol} / 0.1 \text{ L} = 0.5 \text{ M}$).