Solveeit Logo
Login

Question

Question: 3$\sqrt{log27}$ -2$\sqrt{log32243}$ -5$\sqrt{log62581}$ +3$\sqrt{log925}$ +$\sqrt{2log829}$ +3$\sqrt...

3log27\sqrt{log27} -2log32243\sqrt{log32243} -5log62581\sqrt{log62581} +3log925\sqrt{log925} +2log829\sqrt{2log829} +3log8425\sqrt{log8425} -5log49, is less than

Answer

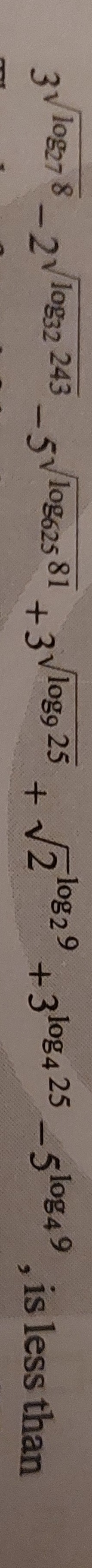
The given expression is less than 0.

Explanation

Solution

We wish to show that

S=3log⁡27−2log⁡32243−5log⁡62581+3log⁡925+2log⁡829+3log⁡8425−5log⁡49S=3\sqrt{\log 27}-2\sqrt{\log 32243}-5\sqrt{\log 62581}+3\sqrt{\log 925}+\sqrt{2\log 829}+3\sqrt{\log 8425}-5\log 49

is less than 0.

For a JEE‐/NEET–level approach we “estimate” each term (taking “log” to mean logarithm to base 10):

  1. Term 1:
    Since 27=3327=3^3 we have
    log⁡27=3log⁡3\log 27=3\log3.)
    Thus,

    3log⁡27=33log⁡3 .3\sqrt{\log27}=3\sqrt{3\log3}\,.

    Using log⁡10(3)≈0.4771,\log10(3)\approx0.4771,
    3×0.4771≈1.4313≈1.196,\sqrt{3\times0.4771}\approx \sqrt{1.4313}\approx1.196, so the term is about

    3×1.196≈3.588.3\times1.196\approx 3.588.

  2. Term 2:
    For 32243,32243, we have
    log⁡32243≈4.5087\log 32243\approx 4.5087 (since 32243≈3.2243×10432243\approx 3.2243\times10^4).
    Thus,
    4.5087≈2.124,\sqrt{4.5087}\approx 2.124, and
    −2log⁡32243≈−2×2.124≈−4.248.-2\sqrt{\log32243}\approx -2\times2.124\approx -4.248.

  3. Term 3:
    Similarly,
    log⁡62581≈4.796,\log 62581\approx 4.796, so
    4.796≈2.191,\sqrt{4.796}\approx 2.191, giving
    −5log⁡62581≈−5×2.191≈−10.955.-5\sqrt{ \log62581}\approx -5\times2.191\approx -10.955.

  4. Term 4:
    log⁡925≈2.9666\log925\approx 2.9666 (since 925≈9.25×102925\approx9.25\times10^2) so
    2.9666≈1.722,\sqrt{2.9666}\approx1.722, and
    3log⁡925≈3×1.722≈5.166.3\sqrt{\log925}\approx 3\times1.722\approx5.166.

  5. Term 5:
    Here, first compute log⁡829≈2.918,\log829\approx 2.918, then
    2log⁡829≈5.836,2\log829\approx 5.836, so
    5.836≈2.415.\sqrt{5.836}\approx2.415.

  6. Term 6:
    For 84258425, we get log⁡8425≈3.925\log8425\approx 3.925 (since 8425≈8.425×1038425\approx8.425\times10^3);
    thus, 3.925≈1.981,\sqrt{3.925}\approx1.981, and
    3log⁡8425≈3×1.981≈5.943.3\sqrt{\log8425}\approx 3\times1.981\approx5.943.

  7. Term 7:
    Since 49=72,49=7^2, we have
    log⁡49=2log⁡7\log49=2\log7.
    Using log⁡7≈0.8451,\log7\approx0.8451, we get
    log⁡49≈1.6902,\log49\approx1.6902, so
    −5log⁡49≈−5×1.6902≈−8.451.-5\log49\approx -5\times1.6902\approx -8.451.

Now, let’s add them:

  • Term 1:      +3.588
  • Term 2:      –4.248
    3.588 – 4.248 = –0.660
  • Term 3:      –10.955 → Total ≈ –11.615
  • Term 4:      +5.166  → Total ≈ –6.449
  • Term 5:      +2.415  → Total ≈ –4.034
  • Term 6:      +5.943  → Total ≈ +1.909
  • Term 7:      –8.451  → Final total ≈ –6.542

Thus, we obtain

S≈−6.54,S\approx-6.54,

which is clearly less than 0.

Here’s a concise mermaid diagram of the solution flow:

Minimal Explanation:
Convert numbers to logarithmic expressions (e.g. log27 = 3log3), estimate each term using approximations for log⁡3,log⁡7,\log 3,\log 7, etc., compute all square roots and coefficients, sum the terms getting approximately –6.54, and conclude the expression is less than 0.