Question

39x²+11x-1=0 find a QE having roots α+3 & β+3.

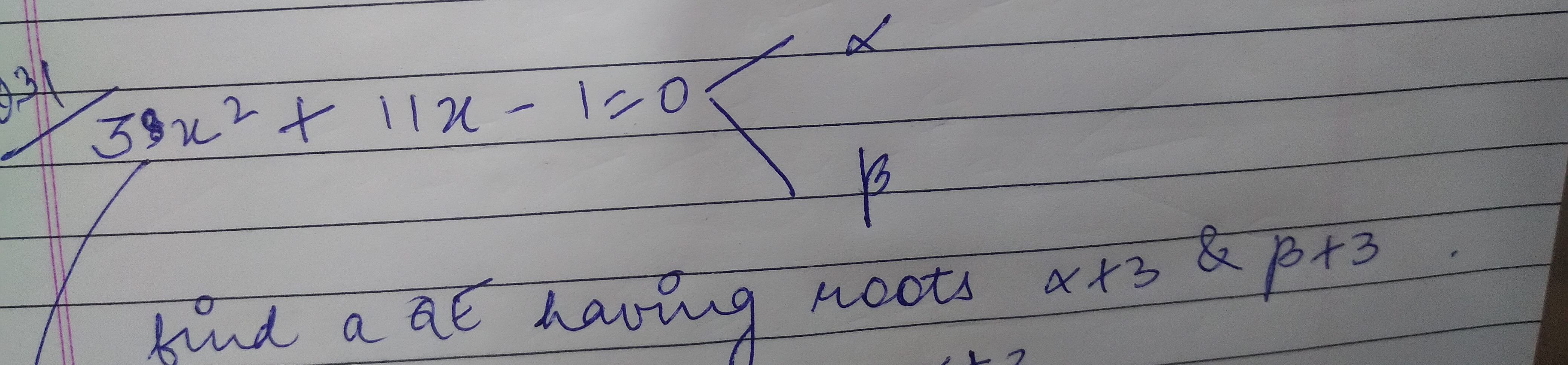
Answer 1

39x² - 223x + 317 = 0

Answer 2

Given the quadratic equation $39x^2 + 11x - 1 = 0$ with roots $\alpha$ and $\beta$. We want to find a new quadratic equation with roots $\alpha' = \alpha+3$ and $\beta' = \beta+3$. Let the new variable be $y$. We use the transformation $y = x+3$, which implies $x = y-3$. Substitute $x = y-3$ into the original equation: $39(y-3)^2 + 11(y-3) - 1 = 0$ $39(y^2 - 6y + 9) + 11y - 33 - 1 = 0$ $39y^2 - 234y + 351 + 11y - 34 = 0$ $39y^2 - 223y + 317 = 0$ Replacing $y$ with $x$ gives the required quadratic equation.