Question

Solve 3cosx + 4sinx = 5

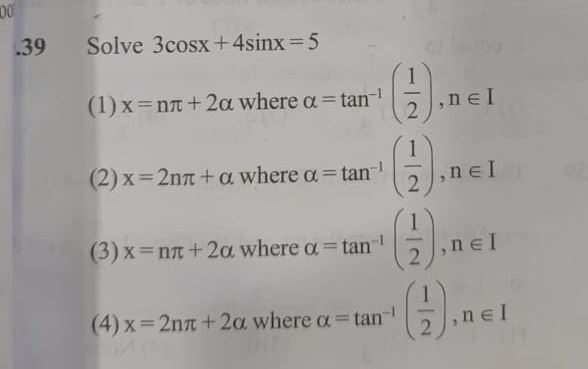
• A. x = nπ + 2α where α = tan⁻¹($\frac{1}{2}$), n ∈ I
• B. x = 2nπ + α where α = tan⁻¹($\frac{1}{2}$), n ∈ I
• C. x = nπ + 2α where α = tan⁻¹($\frac{1}{2}$), n ∈ I
• D. x = 2nπ + 2α where α = tan⁻¹($\frac{1}{2}$), n ∈ I

Answer 1

Answer: (D)

x = 2nπ + 2α where α = tan⁻¹($\frac{1}{2}$), n ∈ I

Answer 2

The given equation is $3\cos x + 4\sin x = 5$. We can solve this using the substitution $t = \tan(x/2)$, where $\cos x = \frac{1-t^2}{1+t^2}$ and $\sin x = \frac{2t}{1+t^2}$. Substituting these into the equation gives $3\left(\frac{1-t^2}{1+t^2}\right) + 4\left(\frac{2t}{1+t^2}\right) = 5$. Multiplying by $(1+t^2)$ yields $3(1-t^2) + 8t = 5(1+t^2)$, which simplifies to $3 - 3t^2 + 8t = 5 + 5t^2$. Rearranging into a quadratic equation gives $8t^2 - 8t + 2 = 0$, or $4t^2 - 4t + 1 = 0$. This factors as $(2t - 1)^2 = 0$, so $t = \frac{1}{2}$. Substituting back $t = \tan(x/2)$, we have $\tan(x/2) = \frac{1}{2}$. Let $\alpha = \tan^{-1}(\frac{1}{2})$. Then $\tan(x/2) = \tan(\alpha)$. The general solution for $\tan \theta = \tan \beta$ is $\theta = n\pi + \beta$. Therefore, $\frac{x}{2} = n\pi + \alpha$, which gives $x = 2n\pi + 2\alpha$. Substituting the value of $\alpha$, we get $x = 2n\pi + 2\tan^{-1}(\frac{1}{2})$.