Solveeit Logo
Login

Question

Question: Simplified form of $\frac{\left(p+\frac{1}{q}\right)^{(p-q)}\left(p-\frac{1}{q}\right)^{(p+q)}}{\lef...

Simplified form of (p+1q)(p−q)(p−1q)(p+q)(q+1p)(p−q)(q−1p)(p+q)=\frac{\left(p+\frac{1}{q}\right)^{(p-q)}\left(p-\frac{1}{q}\right)^{(p+q)}}{\left(q+\frac{1}{p}\right)^{(p-q)}\left(q-\frac{1}{p}\right)^{(p+q)}} =

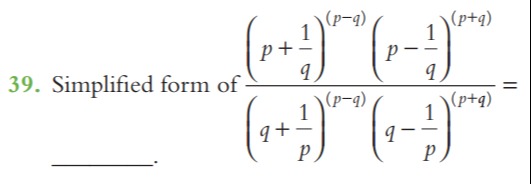
Answer

(pq)2p\left(\frac{p}{q}\right)^{2p}

Explanation

Solution

We start with:

(p+1q)(p−q)(p−1q)(p+q)(q+1p)(p−q)(q−1p)(p+q)\frac{\left(p+\frac{1}{q}\right)^{(p-q)}\left(p-\frac{1}{q}\right)^{(p+q)}}{\left(q+\frac{1}{p}\right)^{(p-q)}\left(q-\frac{1}{p}\right)^{(p+q)}}

Step 1: Rewrite each term as a single fraction:

p+1q=pq+1q,p−1q=pq−1qp+\frac{1}{q}=\frac{pq+1}{q}, \quad p-\frac{1}{q}=\frac{pq-1}{q} q+1p=pq+1p,q−1p=pq−1pq+\frac{1}{p}=\frac{pq+1}{p}, \quad q-\frac{1}{p}=\frac{pq-1}{p}

Step 2: Substitute into the original expression:

(pq+1q)p−q(pq−1q)p+q(pq+1p)p−q(pq−1p)p+q\frac{\left(\frac{pq+1}{q}\right)^{p-q}\left(\frac{pq-1}{q}\right)^{p+q}}{\left(\frac{pq+1}{p}\right)^{p-q}\left(\frac{pq-1}{p}\right)^{p+q}}

Step 3: Combine the exponents by writing numerator and denominator separately:

=(pq+1)p−q(pq−1)p+qq(p−q)+(p+q)⋅p(p−q)+(p+q)(pq+1)p−q(pq−1)p+q=\frac{(pq+1)^{p-q}(pq-1)^{p+q}}{q^{(p-q)+(p+q)}} \cdot \frac{p^{(p-q)+(p+q)}}{(pq+1)^{p-q}(pq-1)^{p+q}} =p2pq2p=\frac{p^{2p}}{q^{2p}}

since (p−q)+(p+q)=2p(p-q)+(p+q)=2p and the common factors (pq+1)p−q(pq−1)p+q(pq+1)^{p-q}(pq-1)^{p+q} cancel.

Step 4: Simplify:

=(pq)2p=\left(\frac{p}{q}\right)^{2p}