Question

Let a computer program generate only the digits 0 and 1 to form a string of binary numbers with probability of occurrence of 0 at even places be $\frac{1}{2}$ and probability of occurrence of 0 at the odd place be $\frac{1}{3}$. Then the probability that '10' is followed by '01' is equal to:

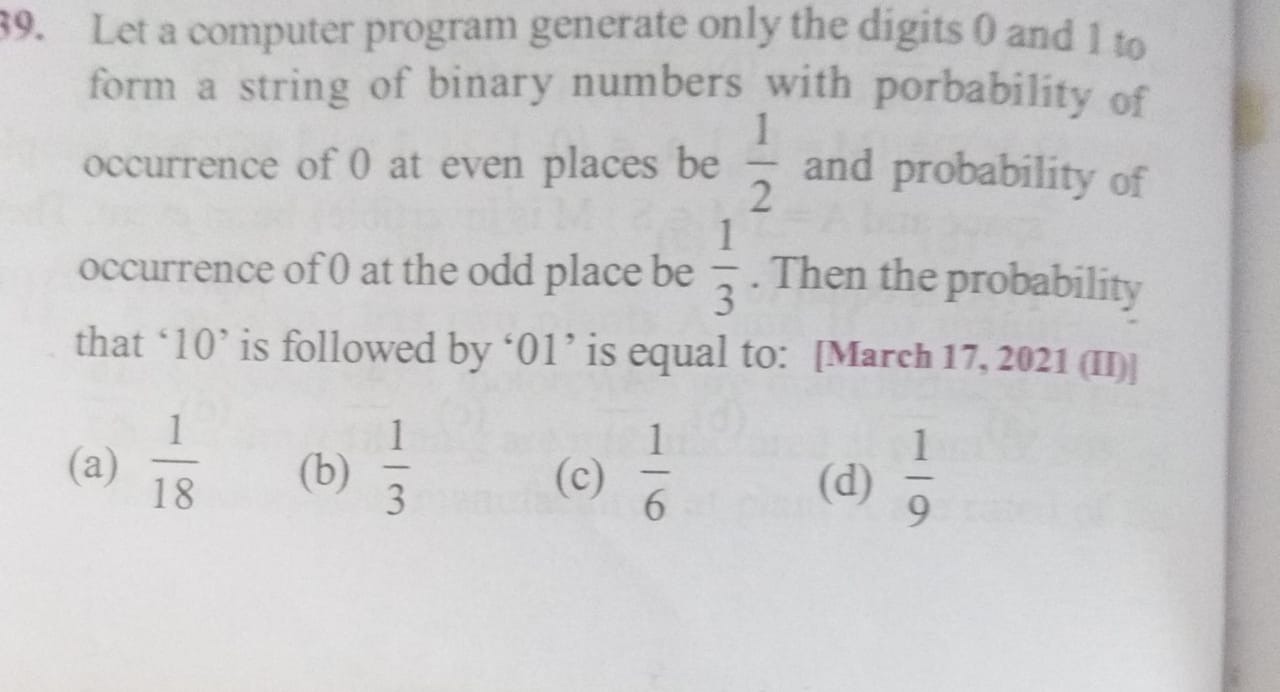
• A. $\frac{1}{18}$
• B. $\frac{1}{3}$
• C. $\frac{1}{6}$
• D. $\frac{1}{9}$

Answer 1

Answer: (A)

$\frac{1}{18}$

Answer 2

The problem asks for the probability of the sequence '1001'. Given probabilities: $P(0 \text{ at odd place}) = \frac{1}{3} \implies P(1 \text{ at odd place}) = 1 - \frac{1}{3} = \frac{2}{3}$ $P(0 \text{ at even place}) = \frac{1}{2} \implies P(1 \text{ at even place}) = 1 - \frac{1}{2} = \frac{1}{2}$

For the sequence '1001' starting at position 1:

• Position 1 (odd): Digit is '1'. Probability = $P(1 \text{ at odd}) = \frac{2}{3}$.
• Position 2 (even): Digit is '0'. Probability = $P(0 \text{ at even}) = \frac{1}{2}$.
• Position 3 (odd): Digit is '0'. Probability = $P(0 \text{ at odd}) = \frac{1}{3}$.
• Position 4 (even): Digit is '1'. Probability = $P(1 \text{ at even}) = \frac{1}{2}$.

Assuming independence, the probability of the sequence '1001' is: $P(\text{'1001'}) = P(1 \text{ at odd}) \times P(0 \text{ at even}) \times P(0 \text{ at odd}) \times P(1 \text{ at even})$ $P(\text{'1001'}) = \frac{2}{3} \times \frac{1}{2} \times \frac{1}{3} \times \frac{1}{2} = \frac{2}{36} = \frac{1}{18}$.