Question

If $\int_{0}^{1} \frac{dx}{\sqrt{1+x}-\sqrt{x}} = \frac{k}{3}$, then $k=$

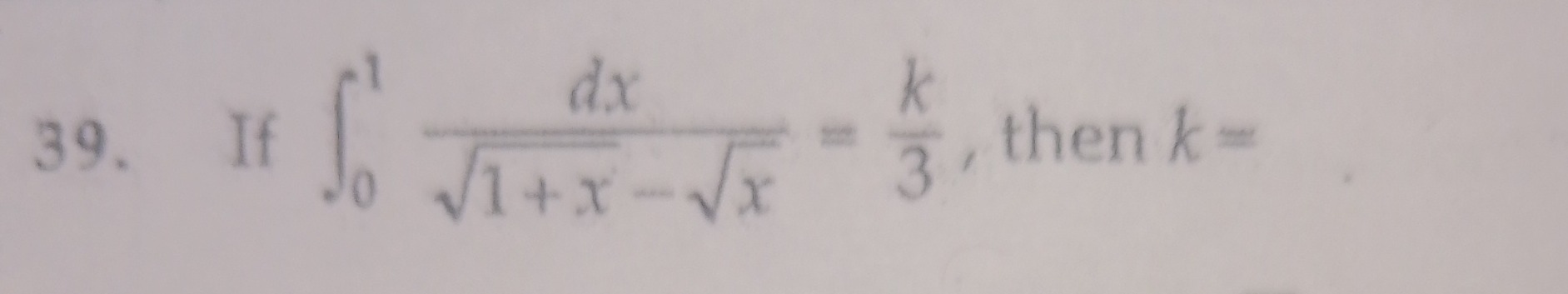
Answer 1

4\sqrt{2}

Answer 2

To solve the integral $\int_{0}^{1} \frac{dx}{\sqrt{1+x}-\sqrt{x}}$, we first rationalize the denominator by multiplying the numerator and denominator by $\sqrt{1+x} + \sqrt{x}$:

$\int_{0}^{1} \frac{dx}{\sqrt{1+x}-\sqrt{x}} = \int_{0}^{1} \frac{\sqrt{1+x}+\sqrt{x}}{(\sqrt{1+x}-\sqrt{x})(\sqrt{1+x}+\sqrt{x})} dx$

$= \int_{0}^{1} \frac{\sqrt{1+x}+\sqrt{x}}{(1+x)-x} dx = \int_{0}^{1} (\sqrt{1+x}+\sqrt{x}) dx$

Now, we split the integral into two parts:

$\int_{0}^{1} \sqrt{1+x} dx + \int_{0}^{1} \sqrt{x} dx$

For the first integral, let $u = 1+x$, so $du = dx$. When $x=0$, $u=1$, and when $x=1$, $u=2$. Thus,

$\int_{1}^{2} \sqrt{u} du = \left[ \frac{2}{3}u^{3/2} \right]_{1}^{2} = \frac{2}{3}(2^{3/2} - 1^{3/2}) = \frac{2}{3}(2\sqrt{2} - 1)$

For the second integral:

$\int_{0}^{1} \sqrt{x} dx = \left[ \frac{2}{3}x^{3/2} \right]_{0}^{1} = \frac{2}{3}(1^{3/2} - 0^{3/2}) = \frac{2}{3}$

Adding the two results:

$\frac{2}{3}(2\sqrt{2} - 1) + \frac{2}{3} = \frac{4\sqrt{2}}{3} - \frac{2}{3} + \frac{2}{3} = \frac{4\sqrt{2}}{3}$

Since $\int_{0}^{1} \frac{dx}{\sqrt{1+x}-\sqrt{x}} = \frac{k}{3}$, we have $\frac{k}{3} = \frac{4\sqrt{2}}{3}$, which implies $k = 4\sqrt{2}$.