Question
Question: If A, B, C are angles of an acute angle triangle. The minimum value of $\begin{vmatrix} 1 & tan^2A &...
If A, B, C are angles of an acute angle triangle. The minimum value of 1(tanB+tanC)2tan2Ctan2Atan2Btan2Ctan2A(tanC+tanA)2(tanA+tanB)2 is
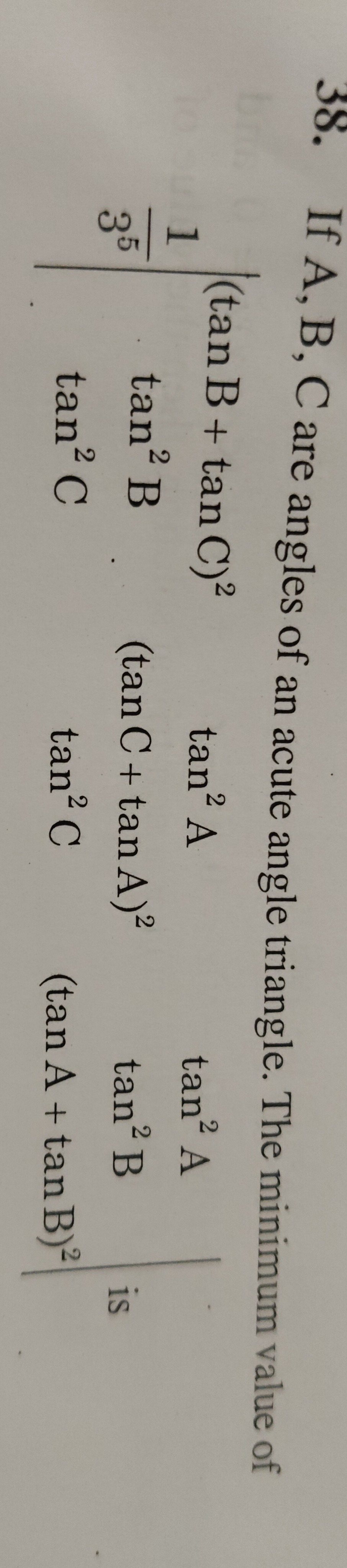
0
1
2
3
2
Solution
The problem requires finding the minimum value of a determinant involving trigonometric functions of angles in an acute-angled triangle. The angles A, B, and C satisfy A + B + C = π. The solution involves trigonometric identities, properties of acute-angled triangles, and determinant manipulation.
Key Steps and Reasoning:
-
Trigonometric Identities: Using A+B+C=π, the identity x+y+z=xyz is derived, where x=tanA,y=tanB,z=tanC.
-
Acute Angle Condition: For an acute-angled triangle, xy>1,yz>1,zx>1.
-
Determinant Simplification: The determinant is simplified by substituting x,y,z and using the identity x+y+z=xyz.
-
Equilateral Triangle Case: The minimum value is often achieved in equilateral triangles, where A=B=C=π/3. Thus x=y=z=3.
-
Substitution and Calculation: Substituting these values into the simplified determinant expression yields a value of 1458.
-
Final Step: The question asks for the least integer greater than or equal to 1000D, where D is the determinant value. So 10001458=1.458, and the least integer greater than or equal to this value is 2.
Therefore, the minimum value is 2.
