Question

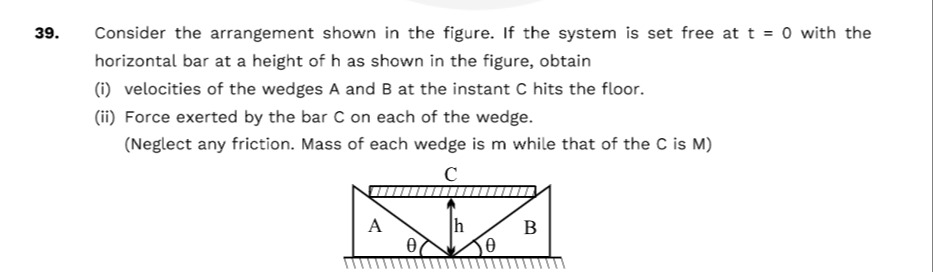
Consider the arrangement shown in the figure. If the system is set free at t = 0 with the horizontal bar at a height of h as shown in the figure, obtain

(i) velocities of the wedges A and B at the instant C hits the floor.

(ii) Force exerted by the bar C on each of the wedge.

(Neglect any friction. Mass of each wedge is m while that of the C is M)

Answer 1

1. The speeds of the left and right wedges are $v_A = v_B = v = \sqrt{\frac{2Mg\,h}{M\tan^2\theta+2m}},$ and the (vertical) speed of the bar (C) when it hits the floor is $V_C = v\,\tan\theta = \tan\theta\sqrt{\frac{2Mg\,h}{M\tan^2\theta+2m}}\,.$

2. The bar exerts on each wedge a normal force given by $N = \frac{mM\,g\cos\theta}{2m\cos^2\theta+M\sin^2\theta}\,.$

Answer 2

1. Geometry & Constraint:
   – Label the distance from the wedge vertex to the point of contact as $r$.
   – Because the bar is horizontal, its vertical coordinate is $y=r\sin\theta$.
   – Initially, $y=h$ so $r=h/\sin\theta$ and when the bar hits the floor $r=0$.
   – The constant bar length gives $L=(x_B-x_A)+2r\cos\theta,$ so differentiating twice (and using symmetry $v_B=-v_A=v$) one obtains
   $\frac{dr}{dt}=-\frac{v}{\cos\theta}\,.$

2. Conservation of Energy:
   – The bar’s center descends by $h$ (loss of potential energy $Mgh$).
   – Its speed is given by $V_C = \frac{dy}{dt} = \frac{dr}{dt}\sin\theta = -\frac{v\sin\theta}{\cos\theta}=-v\tan\theta\,.$ – Kinetic energies are: wedges: $2\cdot\frac12 m v^2 = m v^2$ and bar: $\frac12 M (v\tan\theta)^2$.
   – Energy balance yields

   $$Mgh = \frac12M v^2\tan^2\theta + m v^2,$$

   which rearranges to

   $$v^2=\frac{2Mgh}{M\tan^2\theta+2m}\,.$$

3. Force on the Wedges:
   – The bar exerts on each wedge a normal force $N$ directed perpendicular to the inclined face. Its vertical component is $N\cos\theta$.
   – Writing the vertical force–balance on the bar (it is acted on by its weight $Mg$ downward and two upward components $N\cos\theta$) and noting that at the instant of impact the bar has a downward acceleration $a_y = -v\tan\theta$ (found from differentiating the constraint) leads to

   $$2N\cos\theta - Mg = M\,a_y \,.$$

   – Meanwhile, each wedge (of mass $m$ ) is accelerated horizontally by the horizontal component $N\sin\theta$. Thus

   $$m\,a=N\sin\theta \quad\Longrightarrow\quad a=\frac{N}{m}\sin\theta\,.$$

   – Eliminating the (unknown) acceleration between the two equations gives after some algebra

   $$N=\frac{mM\,g\cos\theta}{2m\cos^2\theta+M\sin^2\theta}\,.$$