Question
Question: Let $P(2, 1,5)$ be a point in space and $Q$ be a point on the line $\vec{r} = (\hat{i} - \hat{j} + 2...
Let P(2,1,5) be a point in space and Q be a point on the line r=(i^−j^+2k^)+μ(−3i^+j^+5k^). Then the value of μ for which the vector PQ is parallel to the plane 3x−y+4z=1 is
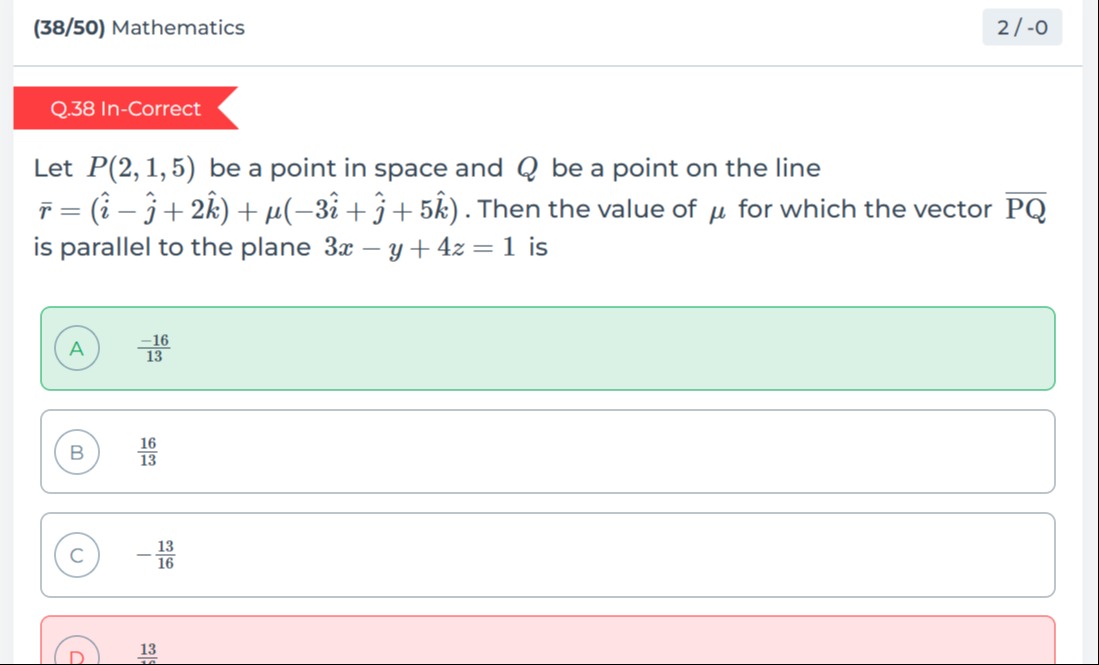
\frac{-16}{13}
\frac{16}{13}
\frac{-13}{16}
\frac{13}{16}
The correct value of μ is 1013 (none of the given options).
Solution
Solution:
-
Coordinates of Q:
r=(1,−1,2)+μ(−3,1,5).
The line is given byHence,
Q=(1−3μ,−1+μ,2+5μ). -
Vector PQ:
PQ=Q−P=((1−3μ)−2,(−1+μ)−1,(2+5μ)−5)=(−1−3μ,−2+μ,−3+5μ).
Point P=(2,1,5), so -
Condition for Parallelism:
3x−y+4z=1,
A vector is parallel to a plane if it is perpendicular to the plane’s normal.
The plane isso its normal is
n=(3,−1,4).Therefore,
PQ⋅n=0. -
Dot Product Calculation:
(−1−3μ)(3)+(−2+μ)(−1)+(−3+5μ)(4)=0.Expanding:
−3−9μ+2−μ−12+20μ=0.Combine like terms:
(−3+2−12)+(−9μ−μ+20μ)=−13+10μ=0.Thus,
10μ=13⟹μ=1013. -
Observing the Options:
The computed answer 1013 does not match any of the provided options (A: −1316, B: 1316, C: −1613, D: 1613). Hence, the correct value is 1013.
Minimal Explanation:
Express Q in terms of μ; compute PQ=Q−P; require PQ to be perpendicular to the normal (3,−1,4); solve (−1−3μ)3+(−2+μ)(−1)+(−3+5μ)4=0 to get μ=1013.
