Question

The shortest distance between $(1-x)^2 + (x-y)^2 + (y-z)^2 + z^2 = \frac{1}{4}$ and $4x+2y+4z+7=0$ in 3-dimensional coordinates system is equal to ____.

Answer 1

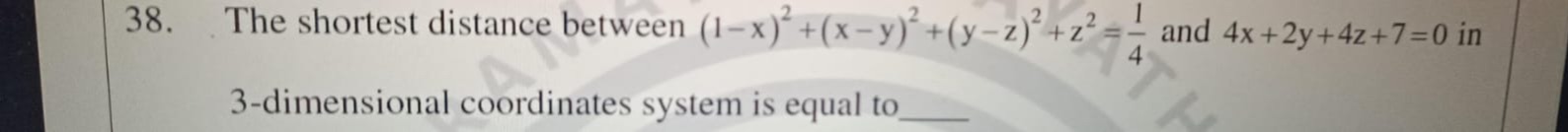
2

Answer 2

The given equation of the surface is $(1-x)^2 + (x-y)^2 + (y-z)^2 + z^2 = \frac{1}{4}$.

Let $u_1 = 1-x$, $u_2 = x-y$, $u_3 = y-z$, $u_4 = z$. The equation becomes $u_1^2 + u_2^2 + u_3^2 + u_4^2 = \frac{1}{4}$. We also note the relationship between these variables: $u_1 + u_2 + u_3 + u_4 = (1-x) + (x-y) + (y-z) + z = 1$.

So, we are looking for points $(x,y,z)$ such that the vector $(u_1, u_2, u_3, u_4) = (1-x, x-y, y-z, z)$ satisfies $u_1^2+u_2^2+u_3^2+u_4^2 = \frac{1}{4}$ and $u_1+u_2+u_3+u_4 = 1$.

Let $\mathbf{u} = (u_1, u_2, u_3, u_4)$. The conditions are $|\mathbf{u}|^2 = \frac{1}{4}$ and $\mathbf{n} \cdot \mathbf{u} = 1$, where $\mathbf{n} = (1,1,1,1)$. The set of vectors $\mathbf{u}$ satisfying these conditions is the intersection of a sphere centered at the origin with radius $1/2$ and a hyperplane defined by $\mathbf{n} \cdot \mathbf{u} = 1$.

The point on the hyperplane $\mathbf{n} \cdot \mathbf{u} = 1$ closest to the origin is the projection of the origin onto the hyperplane. This point is given by $\mathbf{u}_0 = \frac{\mathbf{n}}{|\mathbf{n}|^2}(1) = \frac{(1,1,1,1)}{1^2+1^2+1^2+1^2} (1) = \frac{(1,1,1,1)}{4} = (1/4, 1/4, 1/4, 1/4)$. Let's check if this point lies on the sphere $|\mathbf{u}|^2 = \frac{1}{4}$. $|\mathbf{u}_0|^2 = (1/4)^2 + (1/4)^2 + (1/4)^2 + (1/4)^2 = \frac{1}{16} + \frac{1}{16} + \frac{1}{16} + \frac{1}{16} = \frac{4}{16} = \frac{1}{4}$.

Since the point $\mathbf{u}_0 = (1/4, 1/4, 1/4, 1/4)$ satisfies both conditions, it is the only point of intersection. This means there is only one vector $(u_1, u_2, u_3, u_4)$ that satisfies the given constraints, which is $(1/4, 1/4, 1/4, 1/4)$.

Now we find the corresponding point $(x,y,z)$ from $u_1, u_2, u_3, u_4$: $z = u_4 = 1/4$. $y-z = u_3 = 1/4 \implies y - 1/4 = 1/4 \implies y = 1/2$. $x-y = u_2 = 1/4 \implies x - 1/2 = 1/4 \implies x = 3/4$. $1-x = u_1 = 1/4 \implies 1 - 3/4 = 1/4$. This is consistent.

So the surface defined by the equation is a single point $(x,y,z) = (3/4, 1/2, 1/4)$.

We need to find the shortest distance between this point $(3/4, 1/2, 1/4)$ and the plane $4x+2y+4z+7=0$. The distance from a point $(x_0, y_0, z_0)$ to a plane $Ax+By+Cz+D=0$ is given by the formula $\frac{|Ax_0+By_0+Cz_0+D|}{\sqrt{A^2+B^2+C^2}}$. Here $(x_0, y_0, z_0) = (3/4, 1/2, 1/4)$ and the plane is $4x+2y+4z+7=0$, so $A=4, B=2, C=4, D=7$.

The distance is $d = \frac{|4(3/4) + 2(1/2) + 4(1/4) + 7|}{\sqrt{4^2+2^2+4^2}}$. $d = \frac{|3 + 1 + 1 + 7|}{\sqrt{16+4+16}} = \frac{|12|}{\sqrt{36}} = \frac{12}{6} = 2$.

The shortest distance between the given surface (which is a single point) and the plane is 2.