Question
Question: Prove that from the equality $\frac{sin^4\alpha}{a}+\frac{cos^4\alpha}{b}=\frac{1}{a+b}$ follows the...
Prove that from the equality asin4α+bcos4α=a+b1 follows the relation; a3sin8α+b3cos8α=(a+b)31.
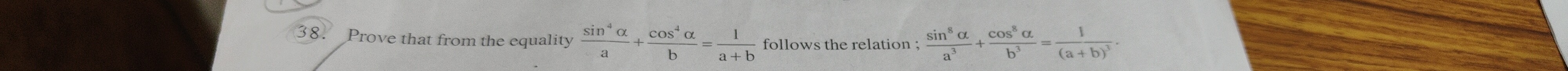
Proven
Solution
To prove the given relation, we start with the initial equality and deduce the values of sin2α and cos2α.
Given equality:
asin4α+bcos4α=a+b1We know that sin2α+cos2α=1. Let x=sin2α and y=cos2α. Then x+y=1. The given equality can be rewritten as:
ax2+by2=a+b(x+y)2This is a specific case of the identity: If AP2+BQ2=A+B(P+Q)2, then it implies AP=BQ. This identity can be proven as follows: Starting from AP2+BQ2=A+B(P+Q)2: Multiply by AB(A+B): B(A+B)P2+A(A+B)Q2=AB(P+Q)2 (AB+B2)P2+(A2+AB)Q2=AB(P2+2PQ+Q2) ABP2+B2P2+A2Q2+ABQ2=ABP2+2ABPQ+ABQ2 Subtract ABP2+ABQ2 from both sides: B2P2+A2Q2=2ABPQ Rearrange the terms: B2P2−2ABPQ+A2Q2=0 This is a perfect square: (BP−AQ)2=0 This implies BP−AQ=0, so BP=AQ. Dividing by AB (assuming A,B=0):
AP=BQApplying this identity to our problem with P=sin2α, Q=cos2α, A=a, B=b: From a(sin2α)2+b(cos2α)2=a+b(sin2α+cos2α)2, it follows that:
asin2α=bcos2αLet this common ratio be k. So, sin2α=ak and cos2α=bk. Using the identity sin2α+cos2α=1: ak+bk=1 k(a+b)=1 k=a+b1 Therefore, we have:
sin2α=a+ba cos2α=a+bbNow, we need to prove the relation a3sin8α+b3cos8α=(a+b)31. Substitute the values of sin2α and cos2α into the left-hand side (LHS) of the relation to be proven:
LHS=a3(sin2α)4+b3(cos2α)4 LHS=a3(a+ba)4+b3(a+bb)4 LHS=a3(a+b)4a4+b3(a+b)4b4 LHS=a3(a+b)4a4+b3(a+b)4b4 LHS=(a+b)4a+(a+b)4b LHS=(a+b)4a+b LHS=(a+b)31This is equal to the right-hand side (RHS) of the relation. Hence, the relation is proven.
