Question
Question: Show that eliminating x & y from the equations, sin x + sin y = a; cos x + cos y = b & tanx + tany =...
Show that eliminating x & y from the equations, sin x + sin y = a; cos x + cos y = b & tanx + tany = c gives (a2+b2)2−4a28ab=c.
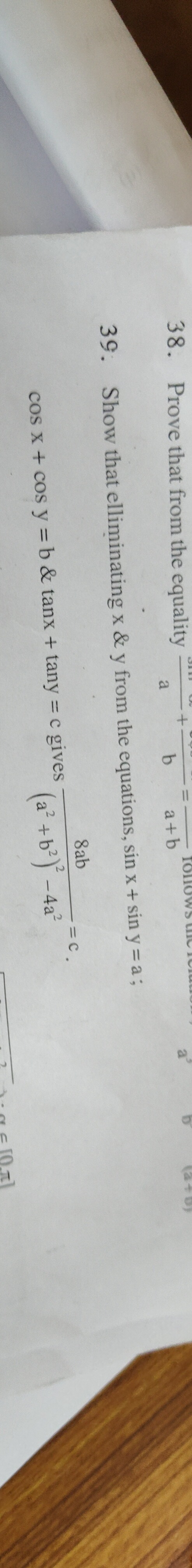
(a2+b2)2−4a28ab=c
Solution
Given equations:
- sinx+siny=a
- cosx+cosy=b
- tanx+tany=c
From (1) and (2), square and add them: (sinx+siny)2+(cosx+cosy)2=a2+b2 (sin2x+sin2y+2sinxsiny)+(cos2x+cos2y+2cosxcosy)=a2+b2 (sin2x+cos2x)+(sin2y+cos2y)+2(sinxsiny+cosxcosy)=a2+b2 1+1+2cos(x−y)=a2+b2 2+2cos(x−y)=a2+b2 cos(x−y)=2a2+b2−2 (Eq. 4)
From (1) and (2), use sum-to-product formulas: 2sin(2x+y)cos(2x−y)=a 2cos(2x+y)cos(2x−y)=b
Divide the first by the second: tan(2x+y)=ba (Eq. 5)
Now, let's work with equation (3): tanx+tany=c cosxsinx+cosysiny=c cosxcosysinxcosy+cosxsiny=c cosxcosysin(x+y)=c (Eq. 6)
We need to express sin(x+y) and cosxcosy in terms of a and b.
From (5), we can find sin(x+y) and cos(x+y) using half-angle identities: sin(x+y)=1+tan2(2x+y)2tan(2x+y)=1+(a/b)22(a/b)=(b2+a2)/b22a/b=a2+b22ab (Eq. 7) cos(x+y)=1+tan2(2x+y)1−tan2(2x+y)=1+(a/b)21−(a/b)2=(b2+a2)/b2(b2−a2)/b2=a2+b2b2−a2 (Eq. 8)
Now, let's find cosxcosy. We use the identity 2cosxcosy=cos(x+y)+cos(x−y). Substitute (4) and (8) into this identity: 2cosxcosy=a2+b2b2−a2+2a2+b2−2 2cosxcosy=2(a2+b2)2(b2−a2)+(a2+b2)(a2+b2−2) 2cosxcosy=2(a2+b2)2b2−2a2+(a2+b2)2−2(a2+b2) 2cosxcosy=2(a2+b2)(a2+b2)2+2b2−2a2−2a2−2b2 2cosxcosy=2(a2+b2)(a2+b2)2−4a2 So, cosxcosy=4(a2+b2)(a2+b2)2−4a2 (Eq. 9)
Finally, substitute (7) and (9) into (6): c=cosxcosysin(x+y)=4(a2+b2)(a2+b2)2−4a2a2+b22ab c=a2+b22ab×(a2+b2)2−4a24(a2+b2) c=(a2+b2)2−4a28ab
This proves the required relation.
