Question

A cubical volume is bounded by the surfaces x = 0, x = a, y = 0, y = a, z = 0, z = a. The electric field in the region is given by $\overrightarrow{E} = E_0x\hat{i}$. Where, $E_0 = 4 \times 10^4 NC^{-1} m^{-1}$. If a = 2 cm, the charge contained in the cubical volume is Q x $10^{-14}$C. The value of Q is _____.(Take $\epsilon_0$ = 9 × $10^{-12}$ $C^2/Nm^2$)

Answer 1

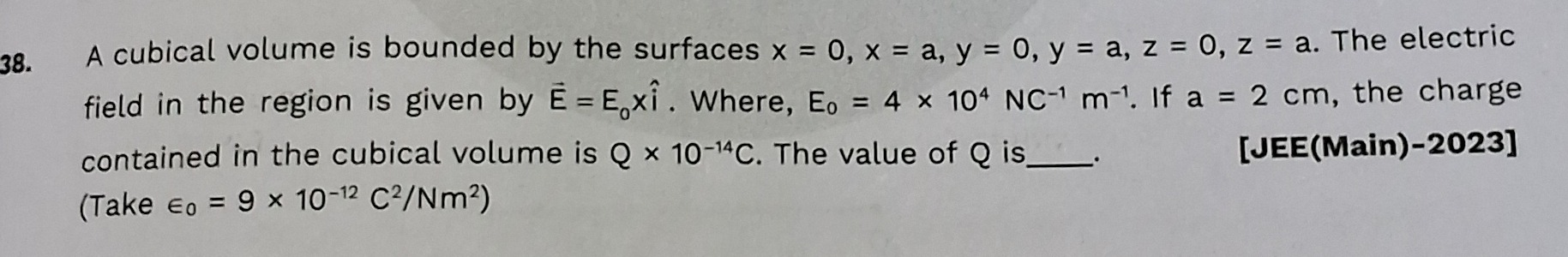
288

Answer 2

The electric field in the region is given by $\overrightarrow{E} = E_0x\hat{i}$.

The cubical volume is bounded by the surfaces $x = 0, x = a, y = 0, y = a, z = 0, z = a$.

We use Gauss's Law to find the charge contained in the volume: $\oint \overrightarrow{E} \cdot d\overrightarrow{A} = \frac{q_{enclosed}}{\epsilon_0}$.

The total electric flux through the closed surface of the cube is the sum of the fluxes through its six faces.

The electric field is in the x-direction ($\hat{i}$).

For the faces perpendicular to the y-axis ($y=0, y=a$) and z-axis ($z=0, z=a$), the area vectors are perpendicular to the electric field ($\hat{j}$ or $\hat{k}$), so the flux through these four faces is zero.

For the face at $x=0$, the electric field is $\overrightarrow{E}(x=0) = E_0(0)\hat{i} = \overrightarrow{0}$. The area vector is $-a^2\hat{i}$. The flux through this face is $\Phi_0 = \overrightarrow{E} \cdot \overrightarrow{A} = \overrightarrow{0} \cdot (-a^2\hat{i}) = 0$.

For the face at $x=a$, the electric field is $\overrightarrow{E}(x=a) = E_0a\hat{i}$. The area vector is $+a^2\hat{i}$. The flux through this face is $\Phi_a = \overrightarrow{E} \cdot \overrightarrow{A} = (E_0a\hat{i}) \cdot (a^2\hat{i}) = E_0a^3$.

The total electric flux through the cube is $\Phi_{net} = \Phi_0 + \Phi_a + \Phi_{y0} + \Phi_{ya} + \Phi_{z0} + \Phi_{za} = 0 + E_0a^3 + 0 + 0 + 0 + 0 = E_0a^3$.

According to Gauss's Law, the charge enclosed is $q_{enclosed} = \epsilon_0 \Phi_{net} = \epsilon_0 E_0 a^3$.

Given values are $E_0 = 4 \times 10^4 NC^{-1} m^{-1}$, $a = 2$ cm $= 2 \times 10^{-2}$ m, and $\epsilon_0 = 9 \times 10^{-12} C^2/Nm^2$.

Substitute the values:

$q_{enclosed} = (9 \times 10^{-12} C^2/Nm^2) \times (4 \times 10^4 NC^{-1} m^{-1}) \times (2 \times 10^{-2} m)^3$

$q_{enclosed} = 9 \times 10^{-12} \times 4 \times 10^4 \times (8 \times 10^{-6}) C$

$q_{enclosed} = (9 \times 4 \times 8) \times 10^{-12 + 4 - 6} C$

$q_{enclosed} = 288 \times 10^{-14} C$.

The problem states that the charge contained in the volume is $Q \times 10^{-14}$ C.

Comparing this with the calculated value, we have $Q \times 10^{-14} C = 288 \times 10^{-14} C$.

Therefore, $Q = 288$.