Question

Two blocks of mass 3 kg and 6 kg respectively are placed on a smooth horizontal surface. The connected by a light spring of force constant k = 200 N/m. Initially the spring is unstretched. indicated velocities are imparted to the blocks. Find the maximum extension of the spring.

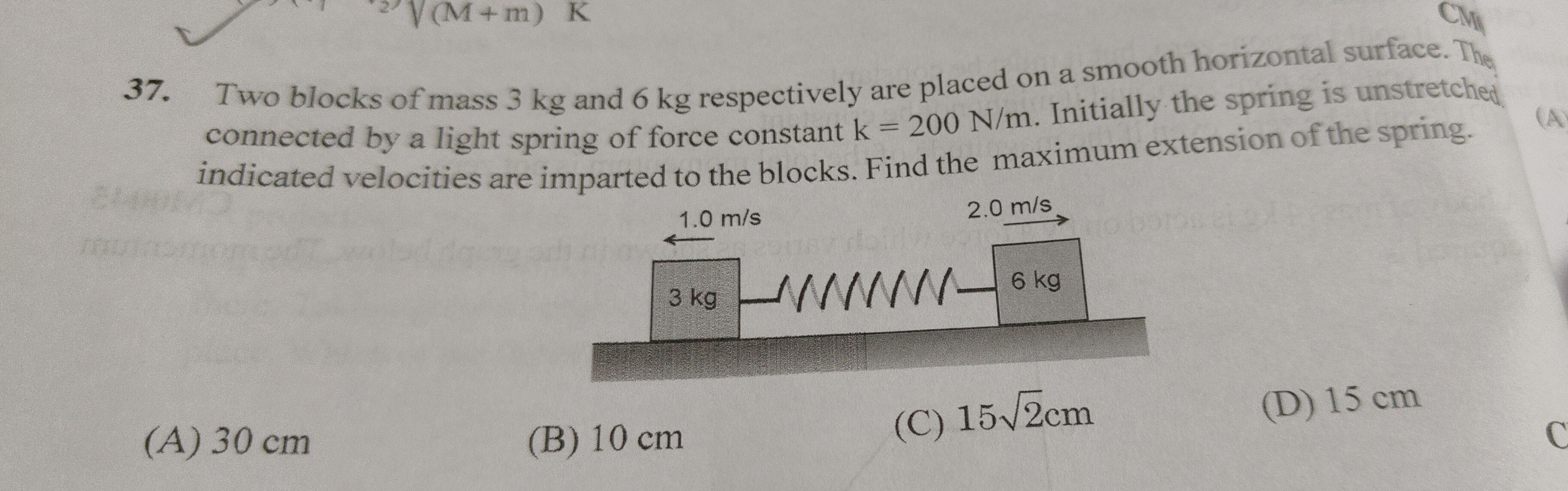
• A. 30 cm
• B. 10 cm
• C. 15$\sqrt{2}$cm
• D. 15 cm

Answer 1

Answer: (A)

30 cm

Answer 2

To find the maximum extension of the spring, we use the principles of conservation of linear momentum and conservation of mechanical energy.

1. Conservation of Linear Momentum:

At the instant of maximum extension (or compression), both blocks move with a common velocity, let's call it $V_{com}$. Since the surface is smooth, there are no external horizontal forces, and thus, the total linear momentum of the system is conserved.

Let $m_1 = 3$ kg and $m_2 = 6$ kg. Let $u_1 = 1.0$ m/s (to the left, so we take it as negative: $u_1 = -1.0$ m/s). Let $u_2 = 2.0$ m/s (to the right, so we take it as positive: $u_2 = +2.0$ m/s).

According to conservation of linear momentum: $m_1 u_1 + m_2 u_2 = (m_1 + m_2) V_{com}$ $(3 \text{ kg})(-1.0 \text{ m/s}) + (6 \text{ kg})(2.0 \text{ m/s}) = (3 \text{ kg} + 6 \text{ kg}) V_{com}$ $-3 + 12 = 9 V_{com}$ $9 = 9 V_{com}$ $V_{com} = 1.0 \text{ m/s}$

2. Conservation of Mechanical Energy:

Since the surface is smooth, mechanical energy is conserved. The initial energy of the system is purely kinetic, and the final energy (at maximum extension) consists of the kinetic energy of the combined mass and the potential energy stored in the spring.

Initial Mechanical Energy ($E_i$): $E_i = \frac{1}{2} m_1 u_1^2 + \frac{1}{2} m_2 u_2^2 + \text{Initial Spring Potential Energy}$ Since the spring is initially unstretched, its initial potential energy is 0. $E_i = \frac{1}{2} (3 \text{ kg}) (-1.0 \text{ m/s})^2 + \frac{1}{2} (6 \text{ kg}) (2.0 \text{ m/s})^2$ $E_i = \frac{1}{2} (3)(1) + \frac{1}{2} (6)(4)$ $E_i = 1.5 + 12 = 13.5 \text{ J}$

Final Mechanical Energy ($E_f$): At maximum extension $x_{max}$, the blocks move with common velocity $V_{com}$, and the spring has potential energy $\frac{1}{2} k x_{max}^2$. $E_f = \frac{1}{2} (m_1 + m_2) V_{com}^2 + \frac{1}{2} k x_{max}^2$ Given $k = 200$ N/m. $E_f = \frac{1}{2} (3 \text{ kg} + 6 \text{ kg}) (1.0 \text{ m/s})^2 + \frac{1}{2} (200 \text{ N/m}) x_{max}^2$ $E_f = \frac{1}{2} (9)(1) + 100 x_{max}^2$ $E_f = 4.5 + 100 x_{max}^2$

Equating initial and final mechanical energy: $E_i = E_f$ $13.5 = 4.5 + 100 x_{max}^2$ $100 x_{max}^2 = 13.5 - 4.5$ $100 x_{max}^2 = 9$ $x_{max}^2 = \frac{9}{100}$ $x_{max} = \sqrt{\frac{9}{100}}$ $x_{max} = \frac{3}{10} \text{ m}$ $x_{max} = 0.3 \text{ m}$

Converting to centimeters: $x_{max} = 0.3 \times 100 \text{ cm} = 30 \text{ cm}$