Question
Question: The equation $(1-tan\theta)(1+tan\theta)sec^2\theta + 2^{tan^2\theta}=0$ has:...
The equation (1−tanθ)(1+tanθ)sec2θ+2tan2θ=0 has:
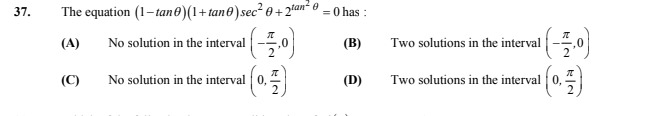
No solution in the interval (−2π,0)
Two solutions in the interval (−2π,0)
No solution in the interval (0,2π)
Two solutions in the interval (0,2π)
B, D
Solution
The given equation is: (1−tanθ)(1+tanθ)sec2θ+2tan2θ=0
First, simplify the terms:
- (1−tanθ)(1+tanθ)=12−tan2θ=1−tan2θ.
- We know that sec2θ=1+tan2θ.
Substitute these into the equation: (1−tan2θ)(1+tan2θ)+2tan2θ=0
Again, apply the difference of squares formula: 12−(tan2θ)2+2tan2θ=0 1−tan4θ+2tan2θ=0
Let x=tan2θ. Since θ∈(−2π,2π), tanθ can take any real value. Therefore, tan2θ=x must be non-negative, i.e., x≥0.
The equation becomes: 1−x2+2x=0 Rearrange the terms: 2x=x2−1
To find the solutions for x, we can analyze the function h(x)=2x−x2+1. We are looking for x≥0 such that h(x)=0.
Let's evaluate h(x) for some non-negative integer values:
- For x=0: h(0)=20−02+1=1−0+1=2.
- For x=1: h(1)=21−12+1=2−1+1=2.
- For x=2: h(2)=22−22+1=4−4+1=1.
- For x=3: h(3)=23−32+1=8−9+1=0.
So, x=3 is a solution.
Let's check for other solutions. Consider the derivative of h(x): h′(x)=dxd(2x−x2+1)=2xln2−2x.
Evaluate h′(x) at x=3: h′(3)=23ln2−2(3)=8ln2−6. Using ln2≈0.693: h′(3)≈8×0.693−6=5.544−6=−0.456. Since h′(3)<0, the function h(x) is decreasing at x=3. This means for x slightly greater than 3, h(x) will become negative.
Let's check h(4): h(4)=24−42+1=16−16+1=1. Since h(3)=0 and h(4)=1, and h(x) is continuous, and h′(3)<0 implies h(x) goes negative after x=3, there must be another root between 3 and 4. To confirm h(x) becomes negative, let's check h(3.2): h(3.2)=23.2−(3.2)2+1≈9.189−10.24+1=−0.051. Since h(3.2)<0 and h(4)=1, by the Intermediate Value Theorem, there exists another root x0∈(3.2,4).
So, we have two distinct solutions for x=tan2θ:
- x=3
- x=x0, where x0∈(3.2,4)
Now, we convert these solutions back to θ:
Case 1: tan2θ=3 tanθ=±3
- If tanθ=3, then θ=3π. This solution lies in the interval (0,2π).
- If tanθ=−3, then θ=−3π. This solution lies in the interval (−2π,0).
Case 2: tan2θ=x0, where x0∈(3.2,4) tanθ=±x0 Since x0∈(3.2,4), we have x0∈(3.2,4)=(3.2,2). Note that 3.2≈1.788.
- If tanθ=x0: Since x0>0, θ=arctan(x0). This solution lies in (0,2π). Since x0=3, this solution is distinct from 3π.
- If tanθ=−x0: Since −x0<0, θ=arctan(−x0)=−arctan(x0). This solution lies in (−2π,0). Since −x0=−3, this solution is distinct from −3π.
In summary:
- In the interval (−2π,0), we have two distinct solutions: θ=−3π and θ=−arctan(x0).
- In the interval (0,2π), we have two distinct solutions: θ=3π and θ=arctan(x0).
Therefore, both options (B) and (D) are correct.
