Question
Question: Light traveling through three transparent substances follows the path shown in the figure. Assuming ...
Light traveling through three transparent substances follows the path shown in the figure. Assuming that total internal reflection does take place on the bottom surface of medium 2, arrange the refractive index in the increasing order.
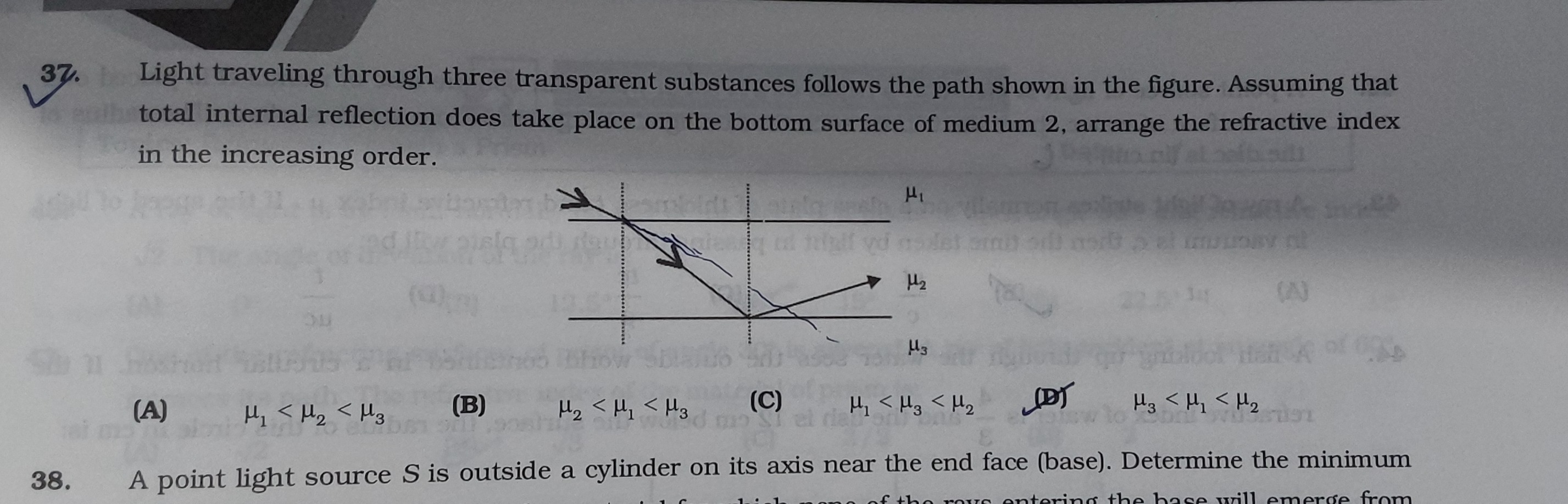
μ1<μ2<μ3
μ2<μ1<μ3
μ1<μ3<μ2
μ3<μ1<μ2
(D)
Solution
To determine the increasing order of refractive indices μ1,μ2,μ3, we analyze the path of light at each interface using Snell's Law and the conditions for Total Internal Reflection (TIR).
Let θ1 be the angle of incidence in medium 1 at the interface with medium 2.
Let θ2 be the angle of refraction in medium 2 at the interface with medium 1. Due to parallel layers, θ2 is also the angle of incidence in medium 2 at the interface with medium 3.
1. Refraction at the interface between Medium 1 and Medium 2:
From the figure, the light ray bends towards the normal as it passes from medium 1 to medium 2.
When light bends towards the normal, it implies that the light is moving from a rarer medium to a denser medium.
Therefore, the refractive index of medium 2 is greater than that of medium 1.
This gives us the first inequality:
μ2>μ1
According to Snell's Law at this interface:
μ1sinθ1=μ2sinθ2
Since the ray bends towards the normal, θ1>θ2.
If θ1>θ2, then sinθ1>sinθ2.
For the equality μ1sinθ1=μ2sinθ2 to hold, it must be that μ2>μ1. This confirms our initial observation.
2. Total Internal Reflection (TIR) at the interface between Medium 2 and Medium 3:
The problem statement explicitly mentions that total internal reflection takes place on the bottom surface of medium 2 (which is the interface between medium 2 and medium 3).
For TIR to occur, two conditions must be met:
(a) Light must travel from a denser medium to a rarer medium.
(b) The angle of incidence must be greater than the critical angle.
From condition (a), for TIR to occur when light travels from medium 2 to medium 3, medium 2 must be denser than medium 3.
Therefore, the refractive index of medium 2 is greater than that of medium 3.
This gives us the second inequality:
μ2>μ3
Now we have established:
μ2>μ1
μ2>μ3
This means μ2 is the largest refractive index among the three. We need to compare μ1 and μ3.
From condition (b) for TIR, the angle of incidence θ2 must be greater than the critical angle C23 for the interface between medium 2 and medium 3.
The critical angle C23 is given by sinC23=μ2μ3.
So, θ2>C23, which implies sinθ2>sinC23.
sinθ2>μ2μ3
From Snell's Law at the first interface, we have sinθ2=μ2μ1sinθ1.
Substitute this into the TIR condition:
μ2μ1sinθ1>μ2μ3
Since μ2 is a positive refractive index, we can multiply both sides by μ2:
μ1sinθ1>μ3
Now, let's analyze this inequality to compare μ1 and μ3:
Since θ1 is an angle of incidence (and not 90 degrees for the ray to travel through the medium), 0<sinθ1≤1.
If μ1=μ3, then μ1sinθ1>μ1. This implies sinθ1>1, which is impossible. So μ1=μ3.
If μ1<μ3, then μ1sinθ1>μ3 would imply sinθ1>μ1μ3. Since μ1<μ3, μ1μ3>1. So sinθ1>(a value greater than 1), which is impossible. So μ1 cannot be less than μ3.
The only remaining possibility is μ1>μ3.
Combining all inequalities:
μ2>μ1
μ1>μ3
μ2>μ3
Therefore, the increasing order of refractive indices is μ3<μ1<μ2.
