Question

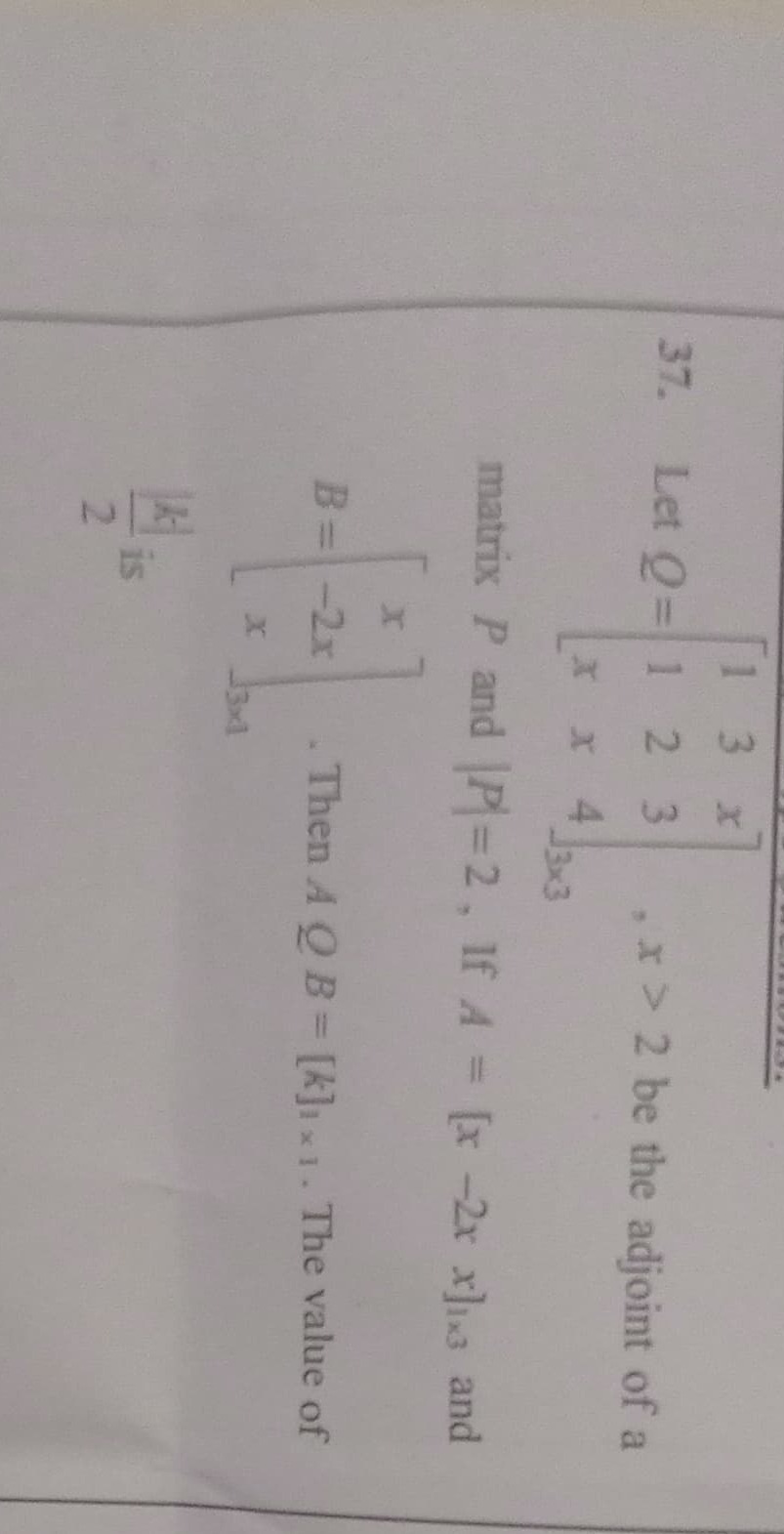
Let $Q = \begin{bmatrix} 1 & 3 & x \\ x & 2 & 3 \\ x & x & 4 \end{bmatrix}_{3x3}$, $x > 2$ be the adjoint of a matrix $P$ and $|P| = 2$, If $A = [x \ -2x \ x]_{1x3}$ and $B = \begin{bmatrix} x \\ -2x \\ x \end{bmatrix}_{3x1}$. Then $AQB = [k]_{1x1}$. The value of $\frac{|k|}{2}$ is

Answer 1

17 + 12√2

Answer 2

The problem involves properties of adjoint matrices and matrix multiplication.

1. Find the determinant of Q in terms of x: Given $Q = \begin{bmatrix} 1 & 3 & x \\ x & 2 & 3 \\ x & x & 4 \end{bmatrix}$. The determinant of $Q$ is: $|Q| = 1(2 \times 4 - 3 \times x) - 3(x \times 4 - 3 \times x) + x(x \times x - 2 \times x)$ $|Q| = 1(8 - 3x) - 3(4x - 3x) + x(x^2 - 2x)$ $|Q| = 8 - 3x - 3x + x^3 - 2x^2$ $|Q| = x^3 - 2x^2 - 6x + 8$

2. Use the property of adjoint matrix determinant: We are given that $Q = \text{adj}(P)$ and $P$ is a $3 \times 3$ matrix (since $Q$ is $3 \times 3$). For an $n \times n$ matrix $P$, we have $|\text{adj}(P)| = |P|^{n-1}$. In this case, $n=3$, so $|Q| = |\text{adj}(P)| = |P|^{3-1} = |P|^2$. Given $|P|=2$, we have $|Q| = 2^2 = 4$.

3. Solve for x: Equating the two expressions for $|Q|$: $x^3 - 2x^2 - 6x + 8 = 4$ $x^3 - 2x^2 - 6x + 4 = 0$ We look for roots of this cubic equation. Testing integer factors of 4, we find that $x=-2$ is a root: $(-2)^3 - 2(-2)^2 - 6(-2) + 4 = -8 - 8 + 12 + 4 = 0$. Since $(x+2)$ is a factor, we perform polynomial division: $(x^3 - 2x^2 - 6x + 4) \div (x+2) = x^2 - 4x + 2$. So, the equation becomes $(x+2)(x^2 - 4x + 2) = 0$. The roots are $x=-2$ or $x^2 - 4x + 2 = 0$. Using the quadratic formula for $x^2 - 4x + 2 = 0$: $x = \frac{-(-4) \pm \sqrt{(-4)^2 - 4(1)(2)}}{2(1)} = \frac{4 \pm \sqrt{16 - 8}}{2} = \frac{4 \pm \sqrt{8}}{2} = \frac{4 \pm 2\sqrt{2}}{2} = 2 \pm \sqrt{2}$. We have three possible values for $x$: $-2$, $2+\sqrt{2}$, $2-\sqrt{2}$. The problem states $x > 2$. $2+\sqrt{2} \approx 2+1.414 = 3.414$, which satisfies $x > 2$. $2-\sqrt{2} \approx 2-1.414 = 0.586$, which does not satisfy $x > 2$. Therefore, $x = 2+\sqrt{2}$.

4. Calculate AQB: We are given $A = [x \ -2x \ x]$ and $B = \begin{bmatrix} x \\ -2x \\ x \end{bmatrix}$. First, calculate $AQ$: $AQ = [x \ -2x \ x] \begin{bmatrix} 1 & 3 & x \\ x & 2 & 3 \\ x & x & 4 \end{bmatrix}$ $AQ = [ (x)(1) + (-2x)(x) + (x)(x) \quad (x)(3) + (-2x)(2) + (x)(x) \quad (x)(x) + (-2x)(3) + (x)(4) ]$ $AQ = [ x - 2x^2 + x^2 \quad 3x - 4x + x^2 \quad x^2 - 6x + 4x ]$ $AQ = [ -x^2 + x \quad x^2 - x \quad x^2 - 2x ]$

   Now, calculate $(AQ)B$: $k = [ -x^2 + x \quad x^2 - x \quad x^2 - 2x ] \begin{bmatrix} x \\ -2x \\ x \end{bmatrix}$ $k = (-x^2 + x)(x) + (x^2 - x)(-2x) + (x^2 - 2x)(x)$ $k = -x^3 + x^2 - 2x^3 + 2x^2 + x^3 - 2x^2$ $k = (-x^3 - 2x^3 + x^3) + (x^2 + 2x^2 - 2x^2)$ $k = -2x^3 + x^2$

5. Substitute the value of x and simplify k: From the cubic equation $x^3 - 2x^2 - 6x + 4 = 0$, we can write $x^3 = 2x^2 + 6x - 4$. Substitute this into the expression for $k$: $k = -2(2x^2 + 6x - 4) + x^2$ $k = -4x^2 - 12x + 8 + x^2$ $k = -3x^2 - 12x + 8$

   Now, substitute $x = 2+\sqrt{2}$: $x^2 = (2+\sqrt{2})^2 = 2^2 + 2(2)\sqrt{2} + (\sqrt{2})^2 = 4 + 4\sqrt{2} + 2 = 6 + 4\sqrt{2}$.

   $k = -3(6 + 4\sqrt{2}) - 12(2 + \sqrt{2}) + 8$ $k = -18 - 12\sqrt{2} - 24 - 12\sqrt{2} + 8$ $k = (-18 - 24 + 8) + (-12\sqrt{2} - 12\sqrt{2})$ $k = -34 - 24\sqrt{2}$

6. Calculate $\frac{|k|}{2}$: $|k| = |-34 - 24\sqrt{2}| = |-(34 + 24\sqrt{2})| = 34 + 24\sqrt{2}$. $\frac{|k|}{2} = \frac{34 + 24\sqrt{2}}{2} = 17 + 12\sqrt{2}$.

The final answer is $\boxed{17 + 12\sqrt{2}}$.