Question

37. $\frac{d}{dx}[cos(1-x^2)^2]=$

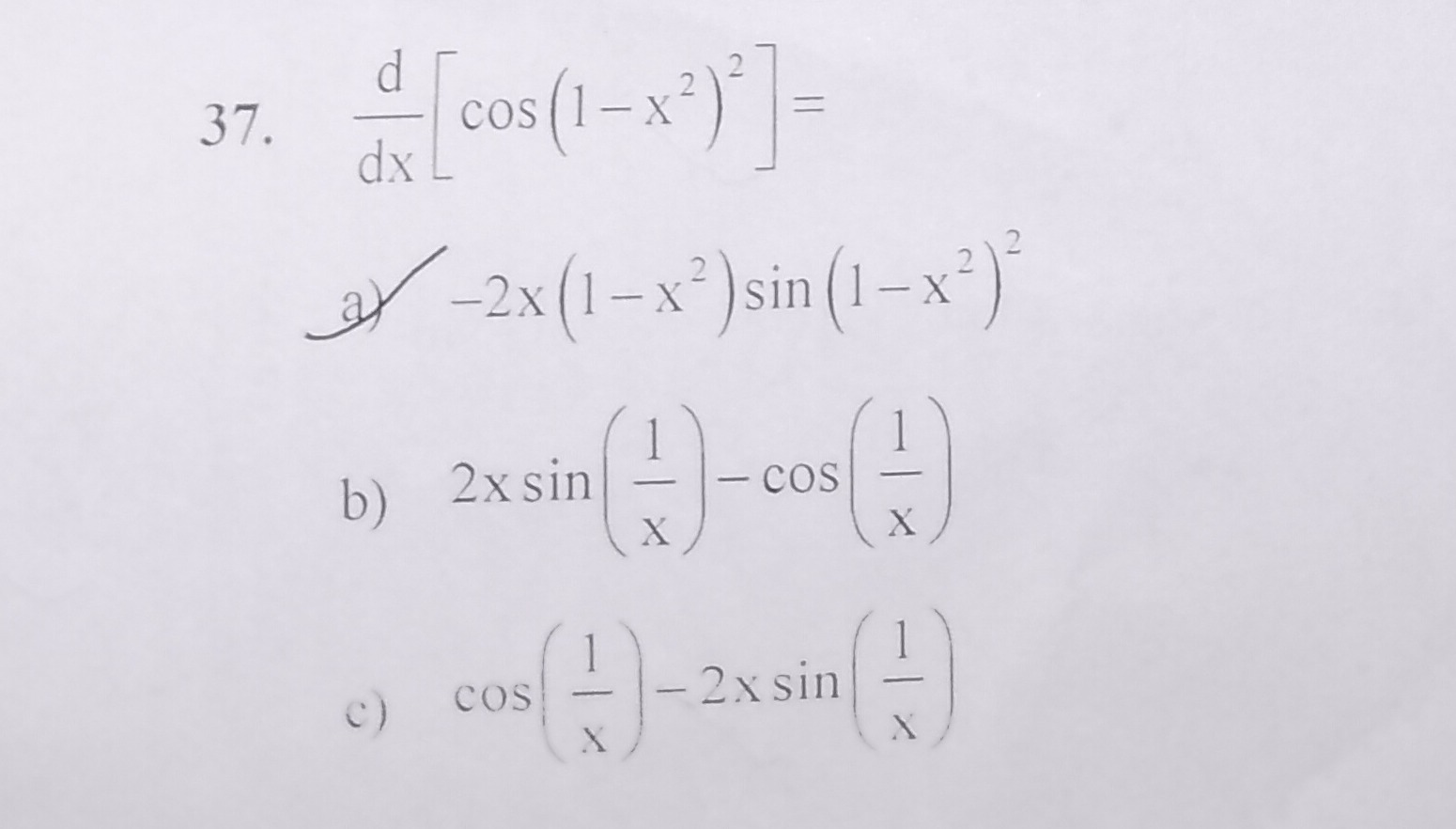
• A. -2x(1-x^2)sin(1-x^2)^2
• B. 2xsin(\frac{1}{x})-cos(\frac{1}{x})
• C. cos(\frac{1}{x})-2xsin(\frac{1}{x})

Answer 1

None of the given options is correct.

Answer 2

Interpreting the expression as
    f(x) = [cos(1 – x²)]²,
we use the chain rule twice. Write
    f(x) = [u(x)]² with u(x) = cos(1 – x²).
Then
    f ′(x) = 2u(x)·u ′(x).
Differentiate u(x):
    u ′(x) = –sin(1 – x²)·d/dx(1 – x²) = –sin(1 – x²)·(–2x) = 2x sin(1 – x²).
Thus,
    f ′(x) = 2 cos(1 – x²) · [2x sin(1 – x²)] = 4x cos(1 – x²) sin(1 – x²).

Alternatively, if one were to interpret the function as
    f(x) = cos[(1 – x²)²],
then by the chain rule
    f ′(x) = –sin[(1 – x²)²]·d/dx[(1 – x²)²].
Since d/dx[(1 – x²)²] = 2(1 – x²)·(–2x) = –4x(1 – x²), we obtain
    f ′(x) = 4x(1 – x²) sin[(1 – x²)²].

In either interpretation neither form matches any of the given options:

• Option (a) gives –2x(1 – x²) sin[(1 – x²)²] (which has a wrong sign and factor).
• Options (b) and (c) involve sin(1/x) and cos(1/x), which are irrelevant here.