Question
Question: Compute the series $\sum_{n=1}^{\infty} \frac{(-1)^{n-1}}{\binom{2n}{2}} = \frac{1}{\binom{2}{2}} -...
Compute the series
∑n=1∞(22n)(−1)n−1=(22)1−(24)1+(26)1−(28)1+(210)1+(212)1+…
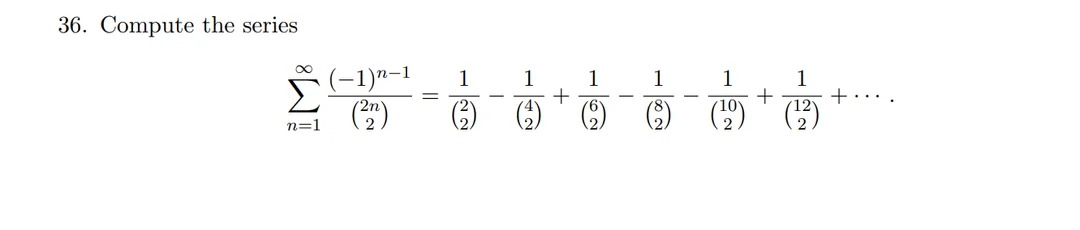
Answer
2π−ln(2)
Explanation
Solution
The series term (22n)(−1)n−1 is simplified using (22n)=n(2n−1). The resulting fraction n(2n−1)1 is decomposed into partial fractions 2n−12−n1. This transforms the original series into two known alternating series: 2∑n=1∞2n−1(−1)n−1 and ∑n=1∞n(−1)n−1. The first sum is 2×arctan(1)=2×4π=2π. The second sum is ln(1+1)=ln(2). Combining these results yields 2π−ln(2).
