Question

Three slabs P, Q, R with different refractive indices are placed as shown. Refractive index of slab R if refracted ray cd is parallel to incident ray ab, is

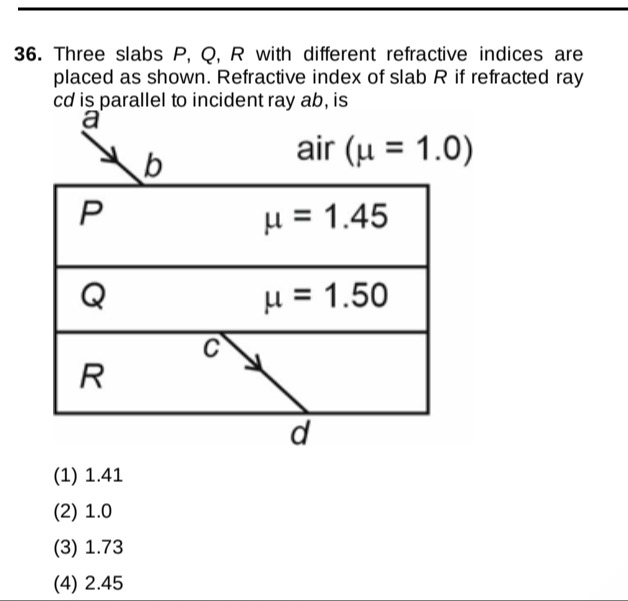
• A. 1.41
• B. 1.0
• C. 1.73
• D. 2.45

Answer 1

Answer: (B)

1.0

Answer 2

We want the ray “cd” in slab R to be parallel to the incident ray “ab” in air. For a plane‐parallel arrangement the emergent ray (or a ray inside slab R if specified) would be parallel to the incident ray only if the last refraction “restores” the original angle. In other words, if “cd” makes an angle equal to the incident angle i with the normal, then, from the final (R–air) boundary we must have

n_R sin r₃ = 1·sin i

But in slab R the ray makes an angle r₃ and we demand that for “cd” to be parallel to “ab” we require r₃ = i.

Substituting we get

n_R sin i = sin i    ⟹  n_R = 1    (provided sin i ≠ 0).

Let us verify the consistency through the successive interfaces. The ray entering slab P (with n = 1.45) from air obeys

sin i = 1.45 sin r₁    ⟹  sin r₁ = sin i/1.45.

At the P–Q interface (slab Q with n = 1.50):

1.45 sin r₁ = 1.50 sin r₂    ⟹  sin r₂ = (1.45/1.50)·(sin i/1.45) = sin i/1.50.

At the Q–R interface:

1.50 sin r₂ = n_R sin r₃    ⟹  1.50 · (sin i/1.50) = n_R sin r₃   ⟹  sin i = n_R sin r₃.

Now, setting r₃ = i gives exactly

sin i = n_R sin i   ⟹  n_R = 1.

Thus the refractive index of slab R is 1.0.

Core Explanation:

Successively apply Snell’s law at each interface. The condition that the ray inside R (angle r₃) is parallel to the incident ray (r₃ = i) forces

n_R sin i = sin i,

hence n_R = 1.