Question

The frequency of revolution of electron in n$^{th}$ Bohr orbit is $v_n$. The graph between log n and log ($v_n/v_1$) may be

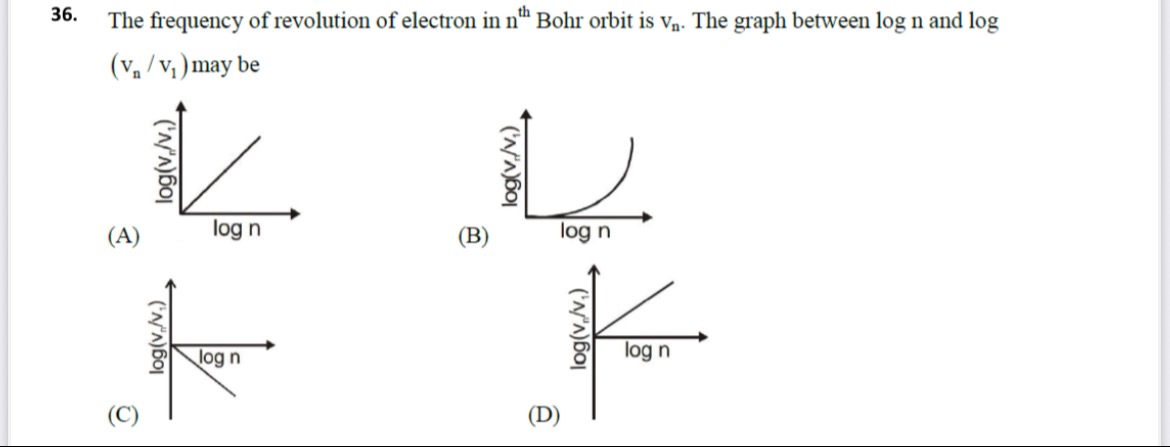
• A. (A)
• B. (B)
• C. (C)
• D. (D)

Answer 1

Answer: (C)

C

Answer 2

The frequency of revolution of an electron in the n$^{th}$ Bohr orbit, denoted as $v_n$, is given by the formula:

$v_n = \frac{\text{velocity of electron in n-th orbit}}{\text{circumference of n-th orbit}} = \frac{v_n}{2 \pi r_n}$

We know the expressions for the velocity ($v_n$) and radius ($r_n$) of an electron in the n$^{th}$ Bohr orbit for a hydrogen-like atom (atomic number Z):

1. Velocity: $v_n = \frac{Z e^2}{2 \epsilon_0 n h}$

   This shows $v_n \propto \frac{Z}{n}$. For a given atom (Z is constant), $v_n \propto \frac{1}{n}$.

2. Radius: $r_n = \frac{n^2 h^2 \epsilon_0}{\pi m_e Z e^2}$

   This shows $r_n \propto \frac{n^2}{Z}$. For a given atom (Z is constant), $r_n \propto n^2$.

Now, substitute these proportionalities into the frequency formula:

$v_n \propto \frac{1/n}{n^2} \propto \frac{1}{n^3}$

So, the frequency of revolution $v_n$ is inversely proportional to the cube of the principal quantum number $n$. We can write this as:

$v_n = K \frac{1}{n^3}$

where K is a constant of proportionality.

For the first Bohr orbit (n=1), the frequency of revolution $v_1$ is:

$v_1 = K \frac{1}{1^3} = K$

Now, let's find the ratio $v_n / v_1$:

$\frac{v_n}{v_1} = \frac{K/n^3}{K} = \frac{1}{n^3}$

We need to find the graph between $\log n$ and $\log (v_n/v_1)$. Let's take the logarithm of both sides of the ratio equation:

$\log \left(\frac{v_n}{v_1}\right) = \log \left(\frac{1}{n^3}\right)$

Using logarithm properties, $\log(1/x) = -\log(x)$ and $\log(x^y) = y \log(x)$:

$\log \left(\frac{v_n}{v_1}\right) = \log (n^{-3})$

$\log \left(\frac{v_n}{v_1}\right) = -3 \log n$

Let $Y = \log \left(\frac{v_n}{v_1}\right)$ and $X = \log n$.

The equation becomes:

$Y = -3X$

This is the equation of a straight line passing through the origin (since Y=0 when X=0) with a negative slope (-3).

Comparing this with the given graphs:

(A) Shows a straight line with a positive slope passing through the origin.

(B) Shows a curve.

(C) Shows a straight line with a negative slope passing through the origin.

(D) Shows a straight line with a positive slope not passing through the origin.

Therefore, graph (C) correctly represents the relationship between $\log n$ and $\log (v_n/v_1)$.