Question
Question: Let $f(x) = 4x(1-x), 0 \leq x \leq 1$. The number of solution of $f(f(f(x))) = \frac{x}{3}$ is:...
Let f(x)=4x(1−x),0≤x≤1. The number of solution of f(f(f(x)))=3x is:
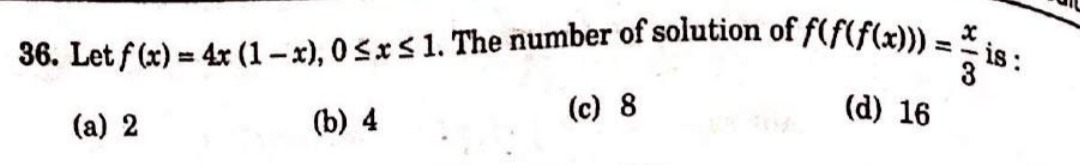
2
4
8
16
8
Solution
Let f(x)=4x(1−x). We want to find the number of solutions for f(f(f(x)))=3x for 0≤x≤1.
Step 1: Use trigonometric substitution.
Let x=sin2θ. Since 0≤x≤1, we can choose θ∈[0,π/2]. Each x corresponds to a unique θ.
Substitute x=sin2θ into f(x): f(x)=4sin2θ(1−sin2θ)=4sin2θcos2θ=(2sinθcosθ)2=(sin2θ)2.
Applying this iteratively: f(f(x))=f((sin2θ)2)=(sin(2⋅2θ))2=(sin4θ)2. f(f(f(x)))=f((sin4θ)2)=(sin(2⋅4θ))2=(sin8θ)2.
Step 2: Rewrite the equation in terms of θ.
The equation becomes (sin8θ)2=3sin2θ. This implies 3sin28θ=sin2θ. Taking the square root of both sides: 3∣sin8θ∣=∣sinθ∣. Since θ∈[0,π/2], sinθ≥0, so ∣sinθ∣=sinθ. Thus, 3∣sin8θ∣=sinθ. This leads to two cases:
Case 1: 3sin8θ=sinθ Case 2: 3sin8θ=−sinθ
Step 3: Analyze the solution x=0.
If x=0, then θ=0. f(f(f(0)))=0 and 0/3=0. So x=0 is a solution. In terms of θ, sin8(0)=0 and sin0=0, so 3∣0∣=0, which is true.
Step 4: Analyze solutions for θ∈(0,π/2).
For θ∈(0,π/2), sinθ>0, so we can divide by sinθ. Let g(θ)=sinθsin8θ. The equations become g(θ)=31 and g(θ)=−31. We know that g(θ)=U7(cosθ), where U7 is the Chebyshev polynomial of the second kind. Let's analyze the graph of g(θ) for θ∈(0,π/2). As θ→0+, g(θ)→8. The roots of g(θ)=0 in (0,π/2) are 8θ=kπ⟹θ=kπ/8 for k=1,2,3. So θ=π/8,π/4,3π/8. The local extrema of g(θ) in (0,π/2) occur at θ=(2k−1)π/16 for k=1,2,3,4. g(π/16)=sin(π/16)sin(π/2)=sin(π/16)1≈5.12 (local maximum). g(3π/16)=sin(3π/16)sin(3π/2)=sin(3π/16)−1≈−1.8 (local minimum). g(5π/16)=sin(5π/16)sin(5π/2)=sin(5π/16)1≈1.2 (local maximum). g(7π/16)=sin(7π/16)sin(7π/2)=sin(7π/16)−1≈−1.02 (local minimum). At θ=π/2, g(π/2)=0.
Let C1=1/3≈0.577 and C2=−1/3≈−0.577.
Counting solutions for g(θ)=C1:
- In (0,π/8): g(θ) starts at 8, decreases to g(π/16)≈5.12, then decreases to 0. It crosses C1≈0.577 once (between π/16 and π/8). (1 solution)
- In (π/8,π/4): g(θ) is negative. No solutions.
- In (π/4,3π/8): g(θ) goes from 0, increases to g(5π/16)≈1.2, then decreases to 0. It crosses C1 twice. (2 solutions)
- In (3π/8,π/2): g(θ) is negative. No solutions. Total solutions for g(θ)=C1 in (0,π/2) is 1+2=3.
Counting solutions for g(θ)=C2:
- In (0,π/8): g(θ) is positive. No solutions.
- In (π/8,π/4): g(θ) goes from 0, decreases to g(3π/16)≈−1.8, then increases to 0. It crosses C2≈−0.577 twice. (2 solutions)
- In (π/4,3π/8): g(θ) is positive. No solutions.
- In (3π/8,π/2): g(θ) goes from 0, decreases to g(7π/16)≈−1.02, then increases to 0. It crosses C2 twice. (2 solutions) Total solutions for g(θ)=C2 in (0,π/2) is 2+2=4.
Step 5: Total number of solutions.
The total number of solutions for θ∈(0,π/2) is 3+4=7. Each of these θ values corresponds to a unique x∈(0,1). Adding the solution x=0 (corresponding to θ=0), the total number of solutions for x is 7+1=8.
The final answer is 8.
