Question
Question: In the figure shown find the acceleration of block A....
In the figure shown find the acceleration of block A.
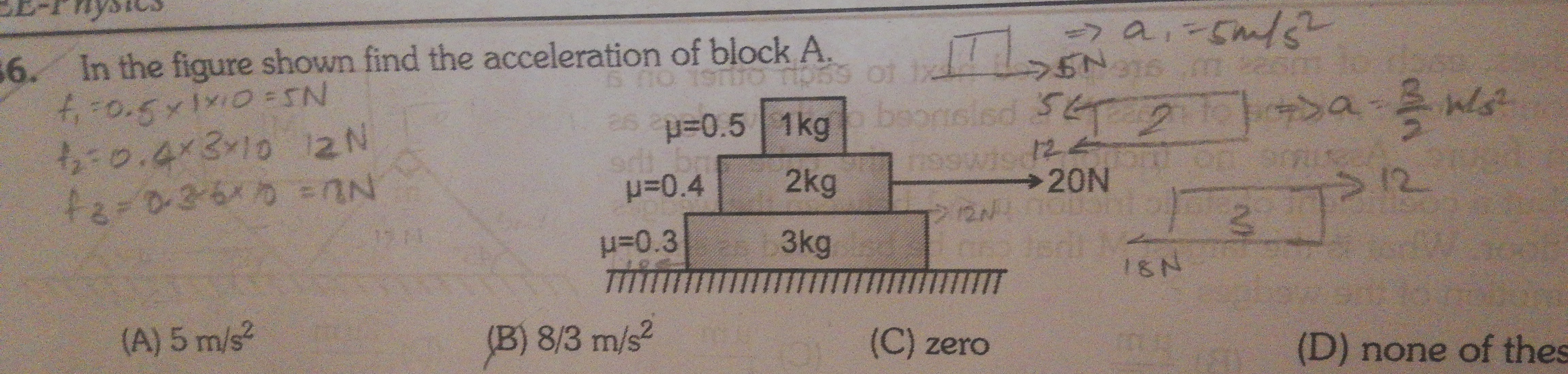
5 m/s²
8/3 m/s²
zero
none of thes
8/3 m/s²
Solution
Let m1=1kg, m2=2kg, m3=3kg. The applied force F=20N is on block 2. The coefficients of friction are μ1=0.5 (between 1 and 2), μ2=0.4 (between 2 and 3), μ3=0.3 (between 3 and ground). Assume g=10m/s2.
Maximum static friction: fs1,max=μ1N1=0.5×(m1g)=0.5×(1×10)=5N. fs2,max=μ2N2=0.4×((m1+m2)g)=0.4×((1+2)×10)=0.4×30=12N. Kinetic friction at the base: fk3=μ3N3=0.3×((m1+m2+m3)g)=0.3×((1+2+3)×10)=0.3×60=18N.
Since F=20N>fk3=18N, the entire system will move.
Let's assume block 1 and 2 move together with acceleration a, and block 3 moves with acceleration a3. For block 1: fs1=m1a=1×a. This friction is from block 2 on block 1. Condition for no slipping between 1 and 2: fs1≤fs1,max⟹a≤5N.
For block 2: F−fs1+fs2=m2a. Here fs1 is from block 1 on block 2 (opposite direction), and fs2 is from block 3 on block 2. 20−a+fs2=2a⟹20+fs2=3a.
For block 3: fs2−fk3=m3a3. Here fs2 is from block 2 on block 3. fs2−18=3a3.
If block 2 and 3 move together, then a3=a. fs2−18=3a⟹fs2=3a+18. Substitute this into the equation for block 2: 20+(3a+18)=3a⟹38=0, which is impossible. This means block 2 slips relative to block 3.
So, block 1 and 2 move together with acceleration a, and block 3 moves with acceleration a3. The friction between block 2 and 3 is kinetic, fs2=fk2=μ2N2=0.4×30=12N. The friction fk2 acts to the left on block 2 and to the right on block 3.
For block 2: F−fs1−fk2=m2a. 20−a−12=2a⟹8=3a⟹a=8/3m/s2.
Now check the condition for block 1: a≤5N. a=8/3m/s2≈2.67m/s2. Since 8/3<5, block 1 does not slip relative to block 2. So, the acceleration of block A is a=8/3m/s2.
Let's find a3: For block 3: fk2−fk3=m3a3. 12−18=3a3⟹−6=3a3⟹a3=−2m/s2. This means block 3 moves backward, which is possible if it's on a very long surface. The question only asks for the acceleration of block A.
The acceleration of block A is 8/3m/s2.
