Question

If $(-\sqrt{2}, \sqrt{2})$ are cartesian co-ordinates of a point, then its polar co-ordinates are

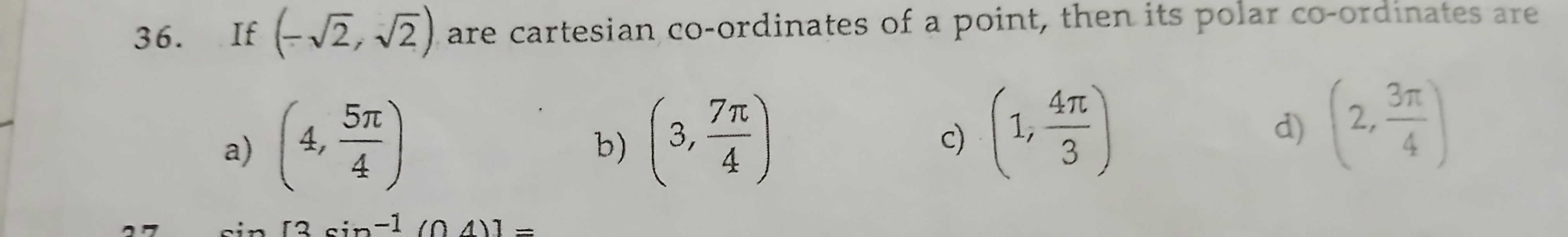
• A. $\left(4, \frac{5\pi}{4}\right)$
• B. $\left(3, \frac{7\pi}{4}\right)$
• C. $\left(1, \frac{4\pi}{3}\right)$
• D. $\left(2, \frac{3\pi}{4}\right)$

Answer 1

Answer: (D)

$\left(2, \frac{3\pi}{4}\right)$

Answer 2

For the point $(-\sqrt{2}, \sqrt{2})$:

1. Compute the radial coordinate:

   $$r = \sqrt{(-\sqrt{2})^2 + (\sqrt{2})^2} = \sqrt{2+2} = 2$$

2. Determine the angle $\theta$:

   Since $x < 0$ and $y > 0$, the point lies in Quadrant II. The reference angle is

   $$\tan^{-1}\left(\frac{|\sqrt{2}|}{|\sqrt{2}|}\right) = \frac{\pi}{4}$$

   Thus, the actual angle is

   $$\theta = \pi - \frac{\pi}{4} = \frac{3\pi}{4}$$

Therefore, the polar coordinates are $(2, \frac{3\pi}{4})$.