Question

36. $\frac{d}{dx}(x^2e^x \sin x) =$

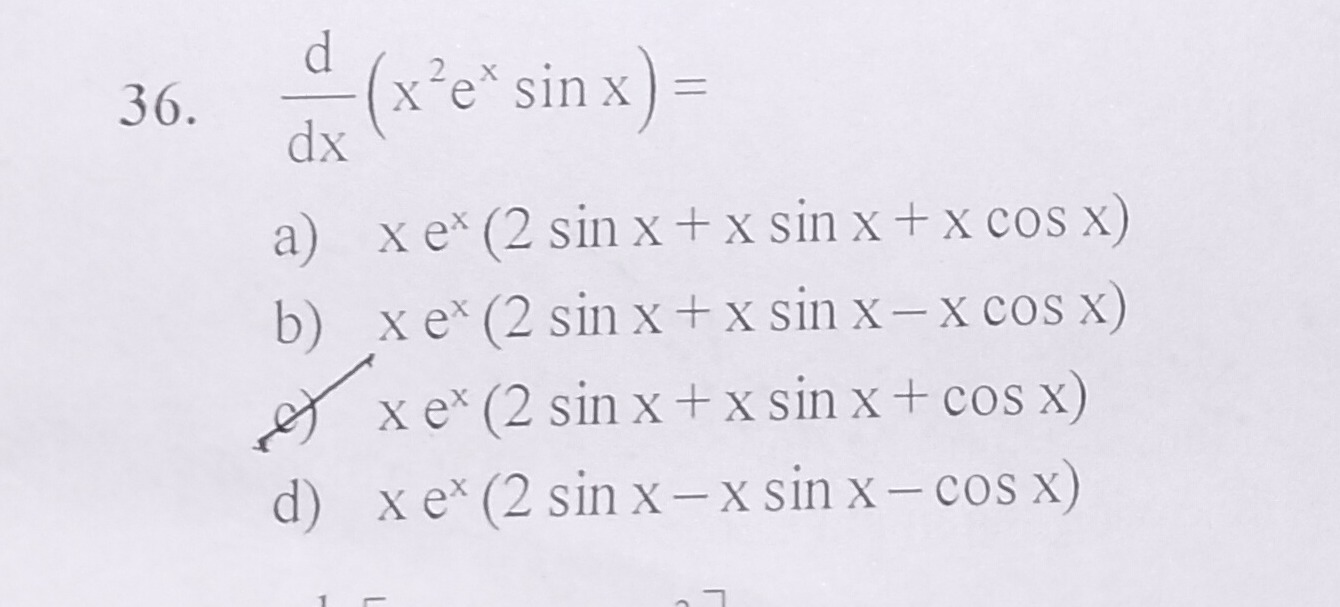
• A. $x e^x (2 \sin x + x \sin x + x \cos x)$
• B. $x e^x (2 \sin x + x \sin x - x \cos x)$
• C. $x e^x (2 \sin x + x \sin x + \cos x)$
• D. $x e^x (2 \sin x - x \sin x - \cos x)$

Answer 1

Answer: (A)

Option (a)

Answer 2

Let

$$u = x^2,\quad v = e^x,\quad w = \sin x.$$

Then,

$$u' = 2x,\quad v' = e^x,\quad w' = \cos x.$$

Using the product rule for three functions:

$$\frac{d}{dx}(uvw) = u'vw + uv'w + uvw',$$

we get:

$$\frac{d}{dx}(x^2 e^x \sin x) = 2x e^x \sin x + x^2 e^x \sin x + x^2 e^x \cos x.$$

Factor out $xe^x$:

$$= xe^x \left(2 \sin x + x \sin x + x \cos x\right).$$