Question: An ant has to travel from point C to A along the gridlines. It gets lost on its way but manages to r...

Question

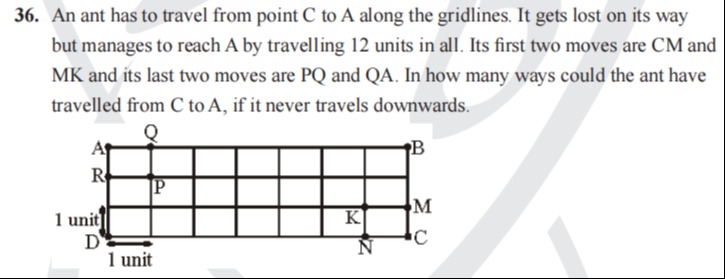
An ant has to travel from point C to A along the gridlines. It gets lost on its way but manages to reach A by travelling 12 units in all. Its first two moves are CM and MK and its last two moves are PQ and QA. In how many ways could the ant have travelled from C to A, if it never travels downwards.

Answer 1

Solution

The problem asks us to find the number of ways an ant can travel from point C to point A on a grid, given several constraints.

First, let's establish the coordinates of the points on the grid, assuming D is at (0,0):

D = (0,0)
R = (0,1)
A = (0,2)
N = (4,0)
C = (5,0)
K = (4,1)
M = (5,1)
P = (1,1)
Q = (1,2)
B = (5,2)

The ant starts at C(5,0) and needs to reach A(0,2).
The constraint "it never travels downwards" means that the y-coordinate of the ant's position can never decrease. Therefore, any vertical move must be an "Up" move (increasing y-coordinate). Allowed moves are Up (U), Left (L), and Right (R). Down (D) moves are forbidden.

Let's analyze the net displacement required to go from C(5,0) to A(0,2):

Net change in x-coordinate: $0 - 5 = -5$ . This means the ant must make 5 more Left moves than Right moves. So, $L_{net} = L - R = 5$ .
Net change in y-coordinate: $2 - 0 = 2$ . Since only Up moves are allowed vertically, the ant must make exactly 2 Up moves. So, $U = 2$ .

The total distance travelled is 12 units. This means the total number of moves is 12.
So, $L + R + U = 12$ .
Substitute $U=2$ :
$L + R + 2 = 12$
$L + R = 10$

Now we have a system of two equations:

$L - R = 5$
$L + R = 10$

Adding (1) and (2):
$(L - R) + (L + R) = 5 + 10$
$2L = 15$
$L = 7.5$

Subtracting (1) from (2):
$(L + R) - (L - R) = 10 - 5$
$2R = 5$
$R = 2.5$

Since the number of moves (L, R, U) must be integers, having $L=7.5$ and $R=2.5$ indicates that the problem statement as given is mathematically impossible under the standard interpretation of grid pathfinding. This often points to a typo in the question, most likely in the total number of units travelled.

Let's assume the question has a typo and the total travel is 11 units instead of 12.
If total moves = 11:
$L + R + U = 11$
$L + R + 2 = 11$
$L + R = 9$

Solving $L - R = 5$ and $L + R = 9$ :
Adding them: $2L = 14 \Rightarrow L = 7$ .
Subtracting them: $2R = 4 \Rightarrow R = 2$ .
So, if the total moves were 11, the ant would make 7 Left moves, 2 Right moves, and 2 Up moves. This is a valid set of integer moves.

Now, let's incorporate the given fixed moves:

First two moves: CM and MK.
- C(5,0) to M(5,1) is an Up move (U).
- M(5,1) to K(4,1) is a Left move (L).
  So, the path starts with U, L. The ant is at K(4,1). 2 moves used.
Last two moves: PQ and QA.
- P(1,1) to Q(1,2) is an Up move (U).
- Q(1,2) to A(0,2) is a Left move (L).
  So, the path ends with U, L. The ant must reach P(1,1) before these moves. 2 moves used.

This means the ant travels from K(4,1) to P(1,1) in the intermediate part of the journey.
Total moves = 11 (assumed typo correction).
Moves used by fixed segments = 2 (start) + 2 (end) = 4 moves.
Intermediate moves = $11 - 4 = 7$ moves.

For the intermediate path from K(4,1) to P(1,1):

Net change in x: $1 - 4 = -3$ . So, $L' - R' = 3$ .
Net change in y: $1 - 1 = 0$ . So, $U' = 0$ . (All vertical moves in intermediate part must be Up, but net change is 0, so no Up moves are needed).

For the intermediate 7 moves:
$L' + R' + U' = 7$
$L' + R' + 0 = 7$
$L' + R' = 7$

Solving $L' - R' = 3$ and $L' + R' = 7$ :
Adding them: $2L' = 10 \Rightarrow L' = 5$ .
Subtracting them: $2R' = 4 \Rightarrow R' = 2$ .
So, the intermediate path consists of 5 Left moves and 2 Right moves.

The number of ways to arrange these 5 Left (L) moves and 2 Right (R) moves is given by the multinomial coefficient formula:
Number of ways = $\frac{\text{Total moves}!}{\text{L moves}! \times \text{R moves}!}$
Number of ways = $\frac{7!}{5! \times 2!} = \frac{7 \times 6}{2 \times 1} = 21$ .

This solution assumes a typo in the question (11 units instead of 12). Without this assumption, the problem leads to non-integer moves, which is impossible for a grid path. Given that such problems usually have integer solutions, it's a reasonable assumption for competitive exams.