Question

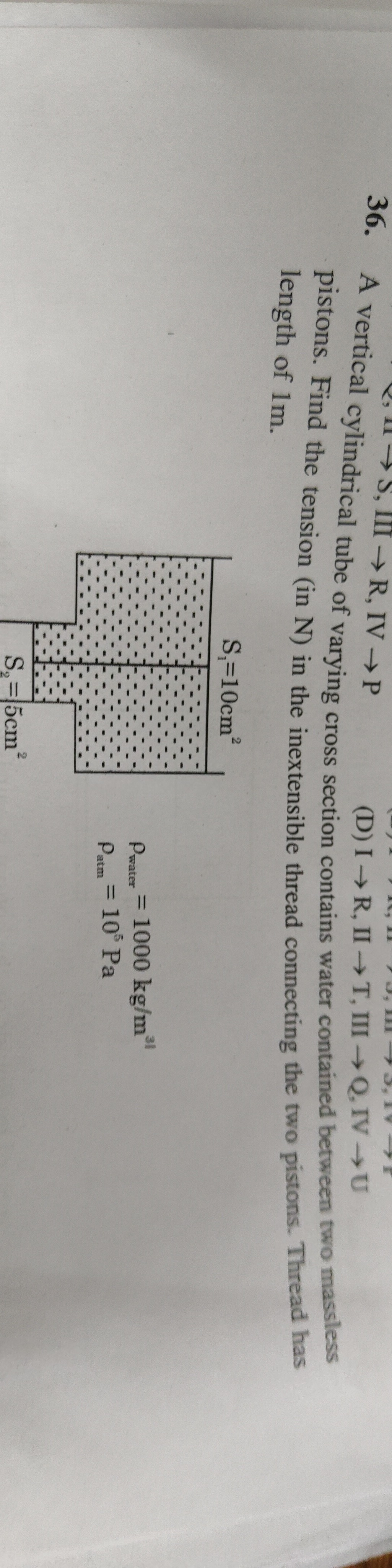
A vertical cylindrical tube of varying cross section contains water contained between two massless pistons. Find the tension (in N) in the inextensible thread connecting the two pistons. Thread has length of 1m.

$S_1$=10cm²

$P_{water}$ = 1000 kg/m³ $P_{atm}$ = $10^5$ Pa

$S_2$=5cm²

• A. I → R, II →T, III →Q. IV → U
• B. Q,S, III → R, IV → P

Answer 1

100

Answer 2

Let $P_{top}$ be the pressure just below the upper piston (area $S_1$) and $P_{bottom}$ be the pressure just above the lower piston (area $S_2$). Assuming the upper piston is at height $y_1$ and the lower piston is at height $y_2$, with $y_1 > y_2$. Forces on the upper piston: $P_{atm}S_1$ downwards, $P_{top}S_1$ upwards, and tension $T$ downwards. Equilibrium for the upper piston: $P_{top}S_1 = P_{atm}S_1 + T \implies P_{top} = P_{atm} + \frac{T}{S_1}$. Forces on the lower piston: $P_{bottom}S_2$ downwards, $P_{atm}S_2$ upwards, and tension $T$ upwards. Equilibrium for the lower piston: $P_{bottom}S_2 + T = P_{atm}S_2 \implies P_{bottom} = P_{atm} - \frac{T}{S_2}$.

However, if the thread is under tension, it would pull the upper piston down and the lower piston up. Let's reconsider the force directions based on the diagram, where $S_1$ is above $S_2$.

Forces on the upper piston: $P_{atm}S_1$ downwards, $P_{top}S_1$ upwards, and tension $T$ upwards. $P_{top}S_1 + T = P_{atm}S_1 \implies P_{top} = P_{atm} - \frac{T}{S_1}$.

Forces on the lower piston: $P_{bottom}S_2$ downwards, $P_{atm}S_2$ upwards, and tension $T$ downwards. $P_{bottom}S_2 + T = P_{atm}S_2 \implies P_{bottom} = P_{atm} - \frac{T}{S_2}$.

Hydrostatic pressure relation: $P_{bottom} = P_{top} + \rho g h$. Substituting the expressions for $P_{top}$ and $P_{bottom}$: $P_{atm} - \frac{T}{S_2} = \left(P_{atm} - \frac{T}{S_1}\right) + \rho g h$ $-\frac{T}{S_2} = -\frac{T}{S_1} + \rho g h$ $T\left(\frac{1}{S_1} - \frac{1}{S_2}\right) = \rho g h$ $T\left(\frac{S_2 - S_1}{S_1 S_2}\right) = \rho g h$ $T = \frac{\rho g h S_1 S_2}{S_2 - S_1}$

Given values: $S_1 = 10 \text{ cm}^2 = 10 \times 10^{-4} \text{ m}^2$ $S_2 = 5 \text{ cm}^2 = 5 \times 10^{-4} \text{ m}^2$ $\rho = 1000 \text{ kg/m}^3$ $g \approx 10 \text{ m/s}^2$ $h = 1 \text{ m}$

$T = \frac{(1000)(10)(1)(10 \times 10^{-4})(5 \times 10^{-4})}{(5 \times 10^{-4}) - (10 \times 10^{-4})} = \frac{10000 \times 50 \times 10^{-8}}{-5 \times 10^{-4}} = \frac{50000 \times 10^{-8}}{-5 \times 10^{-4}} = \frac{5 \times 10^{-4}}{-5 \times 10^{-4}} = -100 \text{ N}$.

A negative tension indicates compression. Since a thread cannot be under compression, let's assume the diagram implies $S_1$ is below $S_2$ or re-evaluate the force directions.

Let's assume the upper piston is at height $y_1$ and the lower piston is at height $y_2$, with $y_1 > y_2$. The thread connects them. Forces on upper piston: $P_{atm}S_1$ downwards, $P_{top}S_1$ upwards, $T$ downwards. $P_{top}S_1 = P_{atm}S_1 + T \implies P_{top} = P_{atm} + T/S_1$. Forces on lower piston: $P_{bottom}S_2$ downwards, $P_{atm}S_2$ upwards, $T$ upwards. $P_{bottom}S_2 + T = P_{atm}S_2 \implies P_{bottom} = P_{atm} - T/S_2$. Hydrostatic relation: $P_{bottom} = P_{top} + \rho g h$. $P_{atm} - T/S_2 = P_{atm} + T/S_1 + \rho g h$ $-T/S_2 - T/S_1 = \rho g h$ $T(-1/S_2 - 1/S_1) = \rho g h$ $T(-(S_1+S_2)/(S_1 S_2)) = \rho g h$ $T = -\frac{\rho g h S_1 S_2}{S_1 + S_2}$. This also yields a negative tension.

Let's assume the upper piston is at height $y_1$ and the lower piston is at height $y_2$, with $y_1 < y_2$. Forces on upper piston: $P_{atm}S_1$ downwards, $P_{top}S_1$ upwards, $T$ upwards. $P_{top}S_1 + T = P_{atm}S_1 \implies P_{top} = P_{atm} - T/S_1$. Forces on lower piston: $P_{bottom}S_2$ downwards, $P_{atm}S_2$ upwards, $T$ downwards. $P_{bottom}S_2 + T = P_{atm}S_2 \implies P_{bottom} = P_{atm} - T/S_2$. Hydrostatic relation: $P_{top} = P_{bottom} + \rho g h$ (since $y_1 < y_2$). $P_{atm} - T/S_1 = (P_{atm} - T/S_2) + \rho g h$ $-T/S_1 = -T/S_2 + \rho g h$ $T(1/S_2 - 1/S_1) = \rho g h$ $T(\frac{S_1 - S_2}{S_1 S_2}) = \rho g h$ $T = \frac{\rho g h S_1 S_2}{S_1 - S_2}$

$T = \frac{(1000)(10)(1)(10 \times 10^{-4})(5 \times 10^{-4})}{(10 \times 10^{-4}) - (5 \times 10^{-4})} = \frac{10000 \times 50 \times 10^{-8}}{5 \times 10^{-4}} = \frac{5 \times 10^{-4}}{5 \times 10^{-4}} = 100 \text{ N}$. This positive tension is consistent with the thread pulling the upper piston down and the lower piston up, which aligns with $S_1$ being above $S_2$ and the pressure decreasing with height.