Question

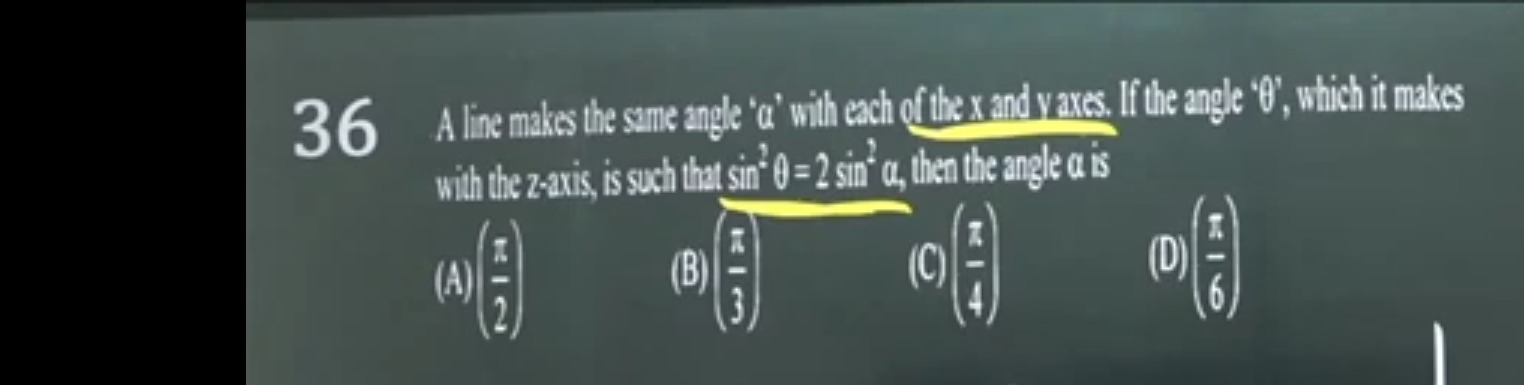
A line makes the same angle '$\alpha$' with each of the x and y axes. If the angle '$\theta$', which it makes with the z-axis, is such that $sin^2\theta = 2sin^2\alpha$, then the angle $\alpha$ is

• A. $\frac{\pi}{2}$
• B. $\frac{\pi}{3}$
• C. $\frac{\pi}{4}$
• D. $\frac{\pi}{6}$

Answer 1

Answer: (C)

$\frac{\pi}{4}$

Answer 2

Let the line have direction cosines:

$$l = \cos\alpha, \quad m = \cos\alpha, \quad n = \cos\theta.$$

Since the line makes the same angle $\alpha$ with the $x$ and $y$ axes. Using the identity for direction cosines:

$$l^2 + m^2 + n^2 = 1 \implies 2\cos^2\alpha + \cos^2\theta = 1 \quad \Longrightarrow \quad \cos^2\theta = 1 - 2\cos^2\alpha.$$

Now, note that

$$\sin^2\theta = 1 - \cos^2\theta = 1 - (1 - 2\cos^2\alpha) = 2\cos^2\alpha.$$

The problem gives:

$$\sin^2\theta = 2\sin^2\alpha = 2(1-\cos^2\alpha).$$

Equate the two expressions for $\sin^2\theta$:

$$2\cos^2\alpha = 2(1-\cos^2\alpha) \implies \cos^2\alpha = 1-\cos^2\alpha \implies 2\cos^2\alpha = 1.$$

Thus,

$$\cos^2\alpha = \frac{1}{2} \quad \Longrightarrow \quad \alpha = \frac{\pi}{4} \quad \text{(since $\alpha$ is acute)}.$$