Question

The real value of x satisfying $\sqrt[3]{20x + \sqrt[3]{20x + 13}} = 13$ can be expressed as $\frac{a}{b}$ where a and b are relatively prime positive integers. Find the value of b?

Answer 1

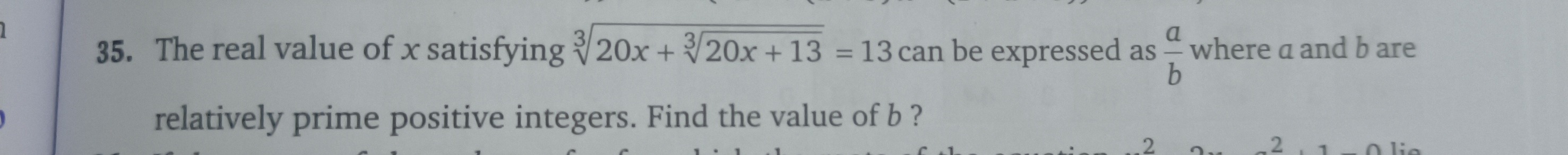
5

Answer 2

To solve the equation $\sqrt[3]{20x + \sqrt[3]{20x + 13}} = 13$, we can use a substitution method.

Let $y = \sqrt[3]{20x + 13}$. Substituting this into the original equation, we get: $\sqrt[3]{20x + y} = 13$

Now, cube both sides of this equation: $20x + y = 13^3$ $20x + y = 2197$ (Equation 1)

Next, from our initial substitution $y = \sqrt[3]{20x + 13}$, cube both sides to eliminate the cube root: $y^3 = 20x + 13$ From this equation, we can express $20x$ in terms of $y$: $20x = y^3 - 13$ (Equation 2)

Now, substitute Equation 2 into Equation 1: $(y^3 - 13) + y = 2197$ $y^3 + y - 13 = 2197$ Rearrange the terms to form a cubic equation: $y^3 + y - 2210 = 0$

We need to find the real roots of this cubic equation. Let $f(y) = y^3 + y - 2210$. We can test integer values for $y$ to find a root. Notice that $13^3 = 2197$. Let's try $y=13$: $f(13) = 13^3 + 13 - 2210$ $f(13) = 2197 + 13 - 2210$ $f(13) = 2210 - 2210$ $f(13) = 0$ So, $y=13$ is a root of the equation.

Since $y=13$ is a root, $(y-13)$ is a factor of $y^3 + y - 2210$. We can perform polynomial division (or synthetic division) to find the other factors: $(y^3 + 0y^2 + y - 2210) \div (y-13) = y^2 + 13y + 170$ So, the cubic equation can be factored as: $(y-13)(y^2 + 13y + 170) = 0$

Now we need to find the roots of the quadratic factor $y^2 + 13y + 170 = 0$. We calculate the discriminant $\Delta = b^2 - 4ac$: $\Delta = (13)^2 - 4(1)(170)$ $\Delta = 169 - 680$ $\Delta = -511$ Since the discriminant $\Delta < 0$, the quadratic equation $y^2 + 13y + 170 = 0$ has no real roots. Therefore, the only real value for $y$ that satisfies the cubic equation is $y=13$.

Now that we have the value of $y$, we can find $x$ using Equation 1: $20x + y = 2197$ Substitute $y=13$: $20x + 13 = 2197$ $20x = 2197 - 13$ $20x = 2184$ $x = \frac{2184}{20}$

To express $x$ as $\frac{a}{b}$ where $a$ and $b$ are relatively prime positive integers, we simplify the fraction: Both the numerator and denominator are divisible by 4: $2184 \div 4 = 546$ $20 \div 4 = 5$ So, $x = \frac{546}{5}$.

Here, $a = 546$ and $b = 5$. Both are positive integers. To check if they are relatively prime, we find their prime factors: Prime factors of 5 are just 5. Prime factors of 546 are $2 \times 3 \times 7 \times 13$. Since 5 is not a factor of 546, $a=546$ and $b=5$ are relatively prime.

The question asks for the value of $b$. From $x = \frac{546}{5}$, the value of $b$ is 5.