Solveeit Logo
Login

Question

Question: 2 gx y X = 35. If $y = \sqrt{x + \sqrt{x + \sqrt{x +........\infty}}}$, then $\frac{dy}{dx}$ is equa...

2 gx y X

  1. If y=x+x+x+........∞y = \sqrt{x + \sqrt{x + \sqrt{x +........\infty}}}, then dydx\frac{dy}{dx} is equal is
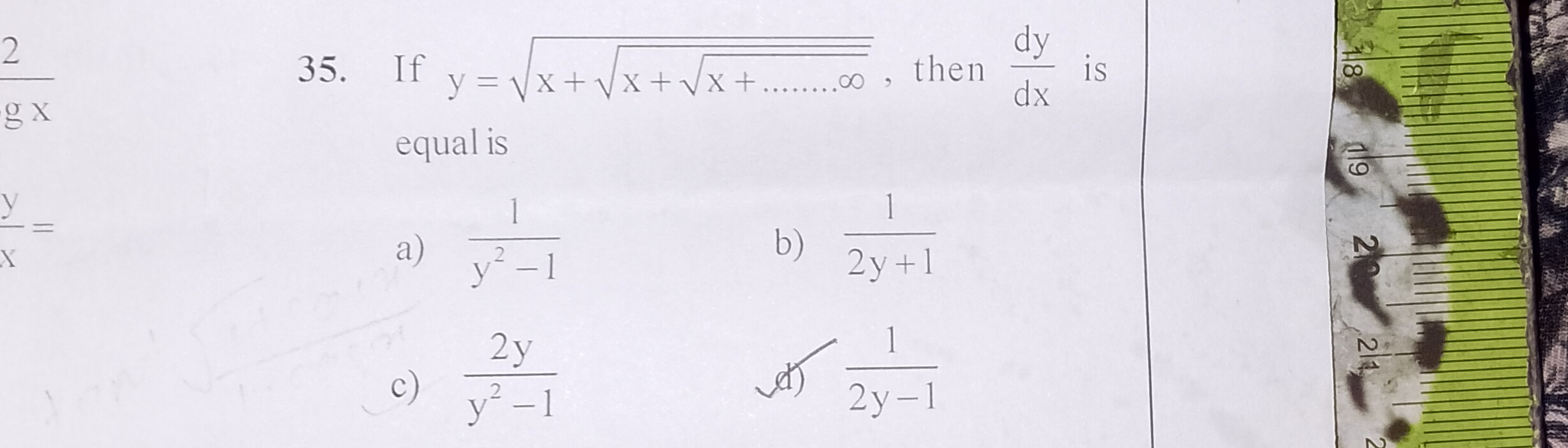
A

1y2−1\frac{1}{y^2-1}

B

12y+1\frac{1}{2y+1}

C

2yy2−1\frac{2y}{y^2-1}

D

12y−1\frac{1}{2y-1}

Answer

12y−1\frac{1}{2y-1}

Explanation

Solution

Given:

y=x+x+x+⋯y = \sqrt{x+\sqrt{x+\sqrt{x+\cdots}}}

Notice that the expression under the square root is again yy, so:

y=x+y⇒y2=x+yy = \sqrt{x+y} \quad \Rightarrow \quad y^2 = x+y

Differentiate both sides with respect to xx:

2ydydx=1+dydx2y\frac{dy}{dx} = 1 + \frac{dy}{dx}

Rearrange:

(2y−1)dydx=1⇒dydx=12y−1(2y - 1)\frac{dy}{dx} = 1 \quad \Rightarrow \quad \frac{dy}{dx} = \frac{1}{2y - 1}