Question

A rod AB is shown in figure. End A of the rod is fixed on the ground. Block is moving with velocity $\sqrt{3}$ m/s towards right. The velocity of end B of rod when rod makes an angle of 60° with the ground is :

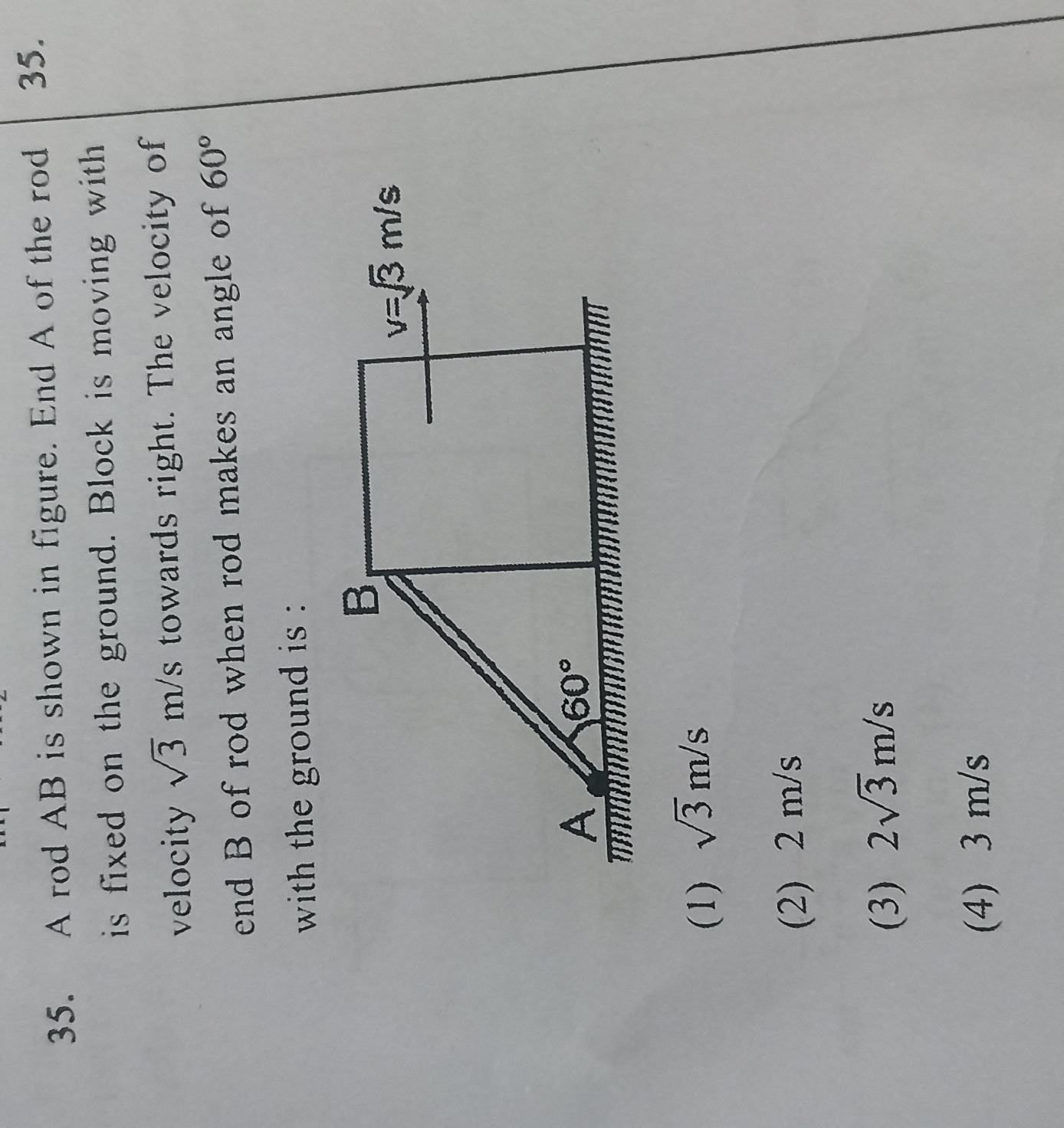
• A. $\sqrt{3}$ m/s
• B. 2 m/s
• C. $2\sqrt{3}$ m/s
• D. 3 m/s

Answer 1

Answer: (B)

2 m/s

Answer 2

Let A be at the origin. Let the length of the rod be $L$. The position of B is $(x,y)$. Given $x = L \cos \theta$ and $y = L \sin \theta$. Differentiating with respect to time, $x v_{Bx} + y v_{By} = 0$. At $\theta = 60^\circ$, $x = L/2$ and $y = L\sqrt{3}/2$. Given $v_{Bx} = \sqrt{3}$ m/s. Substituting these values: $(L/2)(\sqrt{3}) + (L\sqrt{3}/2) v_{By} = 0$. This simplifies to $\sqrt{3} + \sqrt{3} v_{By} = 0$, so $v_{By} = -1$ m/s. The velocity of B is $\vec{v}_B = (\sqrt{3}, -1)$ m/s. The magnitude is $|v_B| = \sqrt{(\sqrt{3})^2 + (-1)^2} = \sqrt{3+1} = 2$ m/s.