Question

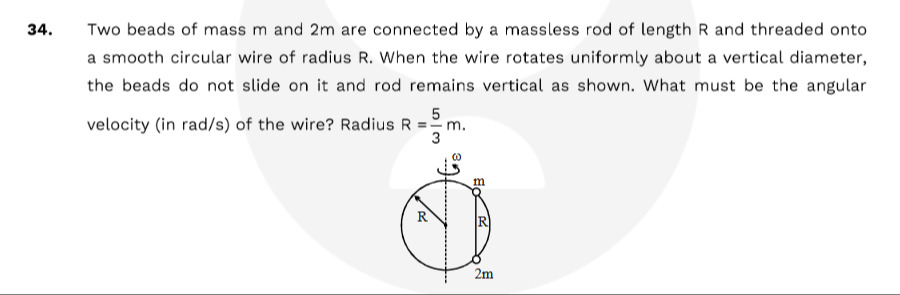
Two beads of mass m and 2m are connected by a massless rod of length R and threaded onto a smooth circular wire of radius R. When the wire rotates uniformly about a vertical diameter, the beads do not slide on it and rod remains vertical as shown. What must be the angular velocity (in rad/s) of the wire? Radius $R = \frac{5}{3}m$.

Answer 1

$\omega=\sqrt{\frac{18g}{5}}\ \text{rad/s}$ or, in general, $\omega=\sqrt{\frac{6g}{R}}$ with $R=\frac{5}{3}$ m.

Answer 2

We wish to find the angular speed ω so that when the two beads (one of mass m and one of mass 2m) are connected by a vertical (massless) rod of length R and are constrained to lie on a smooth circular wire of radius R (in a vertical plane), both beads remain stationary on the wire as it rotates about a vertical diameter.

Because the beads do not slide along the wire the net force along the tangent to the circle (i.e. along the path) must vanish for each bead. In the rotating frame the “effective” forces on a bead are

• its weight (mg downward) and
• the centrifugal force (mω²r horizontally outward),

with r being the horizontal distance from the vertical axis.

A point on the circle can be parameterized by an angle θ (measured from the vertical) so that z = R cosθ and horizontal distance r = R sinθ.

Because the rod is vertical and has length R, if the upper bead is at a height z₁ and the lower bead at z₂ then z₁ – z₂ = R. Since each bead lies on the circle we have R² = (horizontal distance)² + z². For the two beads to have the same horizontal coordinate (i.e. to be aligned vertically) we require that their horizontal distances are equal. A short calculation shows that the only possibility is z₁ = R/2 and z₂ = –R/2. Thus the corresponding angles are:

• for the upper bead: cosθ₁ = (R/2)/R = 1/2 ⟹ θ₁ = 60°,
• for the lower bead: cosθ₂ = (–R/2)/R = –1/2 ⟹ θ₂ = 120°.

In both cases the horizontal distance from the rotation axis is r = R sinθ = R ( (√3)/2 ).

Now, each bead experiences:

• Its weight,
• The centrifugal force,
• A vertical rod force T (the tension or rod force).

The rod force is vertical (upward on bead m and downward on bead 2m).

Let’s write the condition that the net force along the tangent to the circle is zero for each bead. The tangent unit vector (pointing in the direction of increasing θ) at a point characterized by θ is eₜ = (cosθ, 0, –sinθ), when we choose the horizontal axis along the direction of the bead’s horizontal position and the z‐axis vertical.

For the Upper Bead (mass m, θ = 60°)

The forces acting are:

• Weight: mg downward.
• Rod force: T upward.
• Centrifugal force: m ω² (R sin60°) horizontally outward.

Thus the net force is F = m ω² R sinθ i + (–mg + T) k. Its component along eₜ is: F · eₜ = mω²R sinθ cosθ + (–mg + T)(–sinθ) = m ω² R sinθ cosθ + (mg – T) sinθ. Setting F · eₜ = 0 (no tangential motion) and dividing by sinθ (nonzero for θ = 60°): ω² R cosθ + (g – T/m) = 0. For θ = 60° (cos60° = 1/2), we obtain (1) T/m = g + ω² R (1/2).

For the Lower Bead (mass 2m, θ = 120°)

The forces acting are:

• Weight: 2mg downward.
• Rod force: T downward (since the same rod pulls on both beads, but in opposite directions).
• Centrifugal force: 2m ω² (R sin120°) horizontally outward.

(Note: sin120° = sin60° = (√3)/2.) Thus the net force is F = 2mω²R ( (√3)/2 ) i + (–2mg – T) k = mω²R√3 i + (–2mg – T) k. The tangent unit vector at 120° is eₜ = (cos120°, 0, –sin120°) = (–1/2, 0, –(√3)/2). Then: F · eₜ = mω²R√3 + (–2mg – T)(–(√3)/2) = – (mω²R√3)/2 + (2mg + T)(√3)/2. Setting F · eₜ = 0 and multiplying through by 2/√3 gives: – m ω²R + 2mg + T = 0 ⟹ (2) T = mω² R – 2mg.

Equate (1) and (2)

From (1): T = m (g + (ω²R)/2). From (2): T = mω² R – 2mg. Thus, m (g + (ω²R)/2) = mω² R – 2mg. Cancel m: g + (ω²R)/2 = ω²R – 2g. Rearrange: g + 2g = ω²R – (ω²R)/2 ⟹ 3g = (ω²R)/2. Thus, ω² R = 6g ⟹ ω² = 6g/R. So the required angular speed is ω = √(6g/R).

Given R = 5/3 (in meters)

Substitute: ω = √(6g / (5/3)) = √(18g/5).

Core (Minimal) Explanation

1. Positions: For a vertical rod of length R lying on a circle of radius R, the beads must be at z = R/2 and z = –R/2 (θ = 60° and θ = 120°), giving horizontal distance R sin60° = (√3/2)R.

2. Force balance along the tangent (no sliding) for each bead: Write equations for bead m and 2m incorporating weight, centrifugal force, and rod force T.

3. Solve: For bead m: T = m(g + (ω²R)/2). For bead 2m: T = mω²R – 2mg. Equate and solve to get ω² = 6g/R.

4. Substitute numerical R: With R = 5/3, ω = √(18g/5).

Angular speed: $\omega=\sqrt{\frac{18g}{5}}\ \text{rad/s}$ or, in general, $\omega=\sqrt{\frac{6g}{R}}$ with $R=\frac{5}{3}$ m.