Question
Question: The value of $\lim_{x\to\infty} e^{-x} \int_{\frac{1}{x}}^{x+\frac{1}{x}} g(t) \, dt$ equal to :...
The value of limx→∞e−x∫x1x+x1g(t)dt equal to :
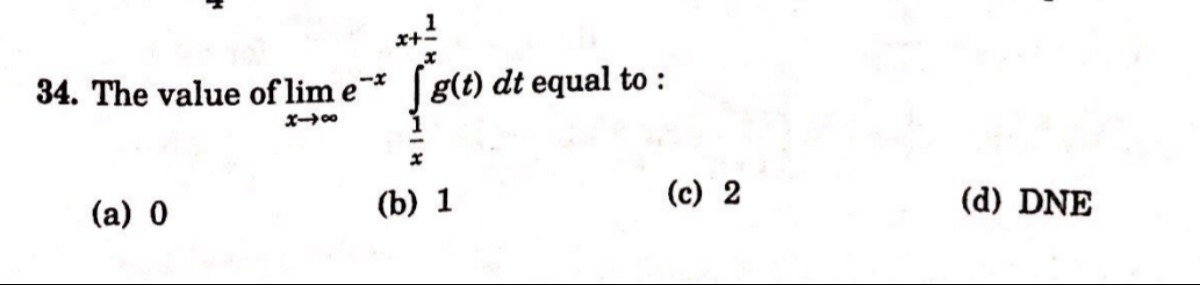
0
1
2
DNE
1
Solution
Let the limit be L. We have L=limx→∞ex∫x1x+x1g(t)dt. This is of the indeterminate form ∞∞ if ∫g(t)dt tends to infinity, or ∞L′ if ∫g(t)dt converges to L′. Consider the case g(t)=et. Then, ∫x1x+x1etdt=[et]x1x+x1=ex+x1−ex1. The limit becomes: L=limx→∞e−x(ex+x1−ex1)=limx→∞(ex+x1e−x−ex1e−x) L=limx→∞(ex1−e−x+x1) As x→∞, x1→0, so ex1→e0=1. As x→∞, −x+x1→−∞, so e−x+x1→0. Therefore, L=1−0=1. While the value of the limit depends on the function g(t), in the context of a multiple-choice question with these options, the case g(t)=et is often the intended scenario that yields a specific numerical answer among the choices. If g(t) grows slower than et, the limit is 0. If g(t) grows faster than et, the limit might be ∞ (DNE). The choice 1 suggests that g(t) grows comparably to et.
