Question

The radius of the circle, having centre at (2, 1), whose one of the chord is a diameter of the circle $x^2+y^2-2x-6y+6=0$

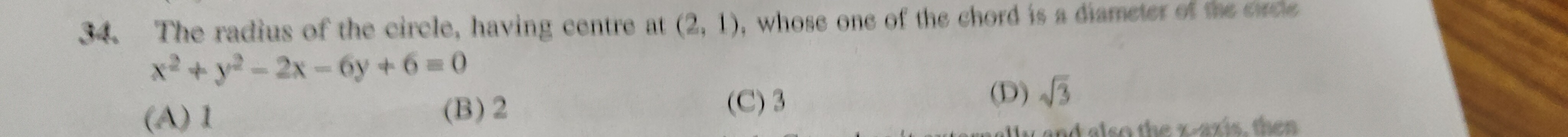
• A. 1
• B. 2
• C. 3
• D. $\sqrt{3}$

Answer 1

Answer: (C)

3

Answer 2

The given circle equation is $x^2+y^2-2x-6y+6=0$. The center of this circle ($C_2$) is found by comparing with the general equation $x^2+y^2+2gx+2fy+c=0$. Here, $2g = -2 \Rightarrow g = -1$, $2f = -6 \Rightarrow f = -3$, and $c = 6$. The center $O_2$ is $(-g, -f) = (1, 3)$. The radius $r_2$ is $\sqrt{g^2+f^2-c} = \sqrt{(-1)^2+(-3)^2-6} = \sqrt{1+9-6} = \sqrt{4} = 2$.

The circle in question ($C_1$) has its center at $O_1=(2, 1)$. A chord of $C_1$ is a diameter of $C_2$. The length of this chord is $2 \times r_2 = 2 \times 2 = 4$. Let $r_1$ be the radius of circle $C_1$. Let $d$ be the perpendicular distance from the center $O_1$ to the chord. In a circle, the radius, half the chord length, and the distance from the center to the chord form a right-angled triangle. So, $r_1^2 = d^2 + (\text{half chord length})^2$. $r_1^2 = d^2 + (4/2)^2 = d^2 + 2^2 = d^2 + 4$.

The distance between the centers $O_1=(2, 1)$ and $O_2=(1, 3)$ is: $d_{centers} = \sqrt{(2-1)^2 + (1-3)^2} = \sqrt{1^2 + (-2)^2} = \sqrt{1+4} = \sqrt{5}$.

For the radius $r_1$ to be uniquely determined, it is implied that the chord (diameter of $C_2$) is perpendicular to the line segment connecting the centers $O_1O_2$ at the point $O_2$. In this specific configuration, the distance $d$ from $O_1$ to the chord is equal to the distance between the centers $O_1O_2$. So, $d = d_{centers} = \sqrt{5}$.

Substituting this value of $d$ into the equation for $r_1^2$: $r_1^2 = (\sqrt{5})^2 + 4 = 5 + 4 = 9$. $r_1 = \sqrt{9} = 3$.