Question

If the value of the definite integral $I = \int_{1}^{\infty}\frac{(2x^3 - 1) dx}{x^6 + 2x^3 + 9x^2 + 1}$ can be expressed in the form $\frac{A}{B}cot^{-1}\frac{C}{D}$ where $\frac{A}{B}$ and $\frac{C}{D}$ are rationals in their lowest form, find the value of $(A + B^2 + C^3 + D^4)$.

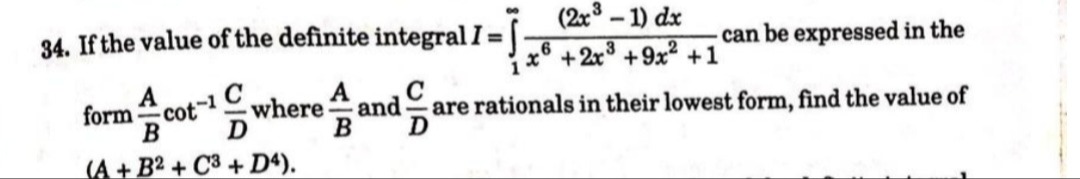
Answer 1

99

Answer 2

The denominator is rewritten as $(x^3+1)^2 + (3x)^2$. Dividing the numerator and denominator by $9x^2$ transforms the integral into $\int \frac{\frac{2x}{9} - \frac{1}{9x^2}}{\left(\frac{x^3+1}{3x}\right)^2 + 1} dx$. Let $u = \frac{x^3+1}{3x}$, then $du = \left(\frac{2x}{3} - \frac{1}{3x^2}\right) dx$. The integral becomes $\frac{1}{3} \int \frac{du}{1+u^2} = \frac{1}{3} \arctan(u)$. Evaluating from $1$ to $\infty$ gives $\frac{\pi}{6} - \frac{1}{3} \arctan(\frac{2}{3})$. Using $\arctan(y) + \operatorname{arccot}(y) = \frac{\pi}{2}$, this simplifies to $\frac{1}{3} \operatorname{arccot}(\frac{2}{3})$. Comparing with $\frac{A}{B}cot^{-1}\frac{C}{D}$, we get $A=1, B=3, C=2, D=3$. Thus, $A + B^2 + C^3 + D^4 = 1 + 3^2 + 2^3 + 3^4 = 1 + 9 + 8 + 81 = 99$.