Question

34. If f (x) = log₂ (log₄ x), then f'(x) at x = 0 is

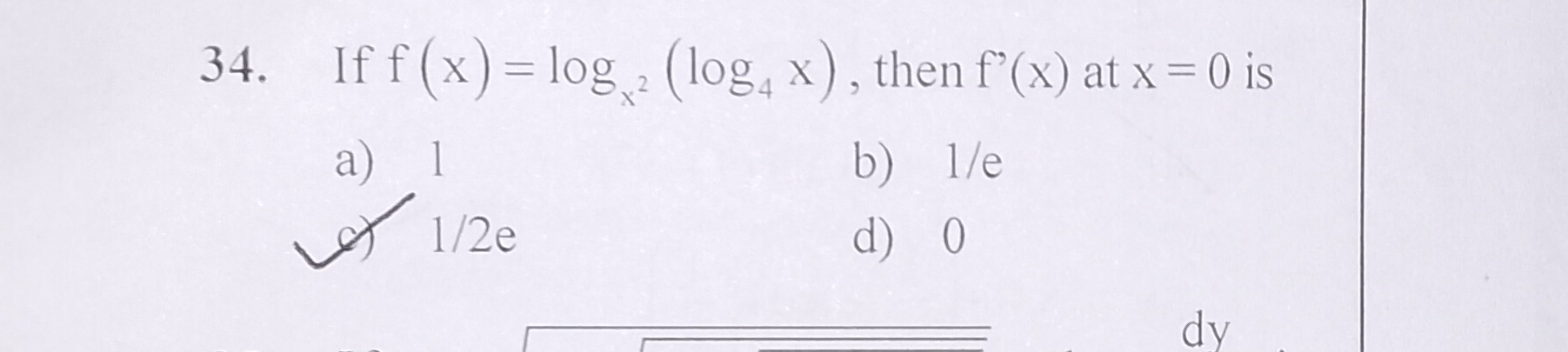
• A. 1
• B. 1/e
• C. 1/2e
• D. 0

Answer 1

The derivative f'(0) is undefined. (None of the given options is correct.)

Answer 2

We have

$$f(x)=\log_2(\log_4 x)=\frac{\ln(\log_4 x)}{\ln2}.$$

Since $\log_4 x=\frac{\ln x}{\ln 4}$, its argument is positive only if $\ln x>0$ (i.e. $x>1$). Thus, the domain of $f(x)$ is $x>1$. Therefore, evaluating $f'(x)$ at $x=0$ is impossible because $0$ is not in the domain of $f$.