Question
Question: If b is very small as compared to the value of a, so that the cube and other higher powers of $\frac...
If b is very small as compared to the value of a, so that the cube and other higher powers of ab can be neglected in the identity a−b1+a−2b1+a−3b1+.....+a−nb1=αn+βn2+γn3, then the value of γ is
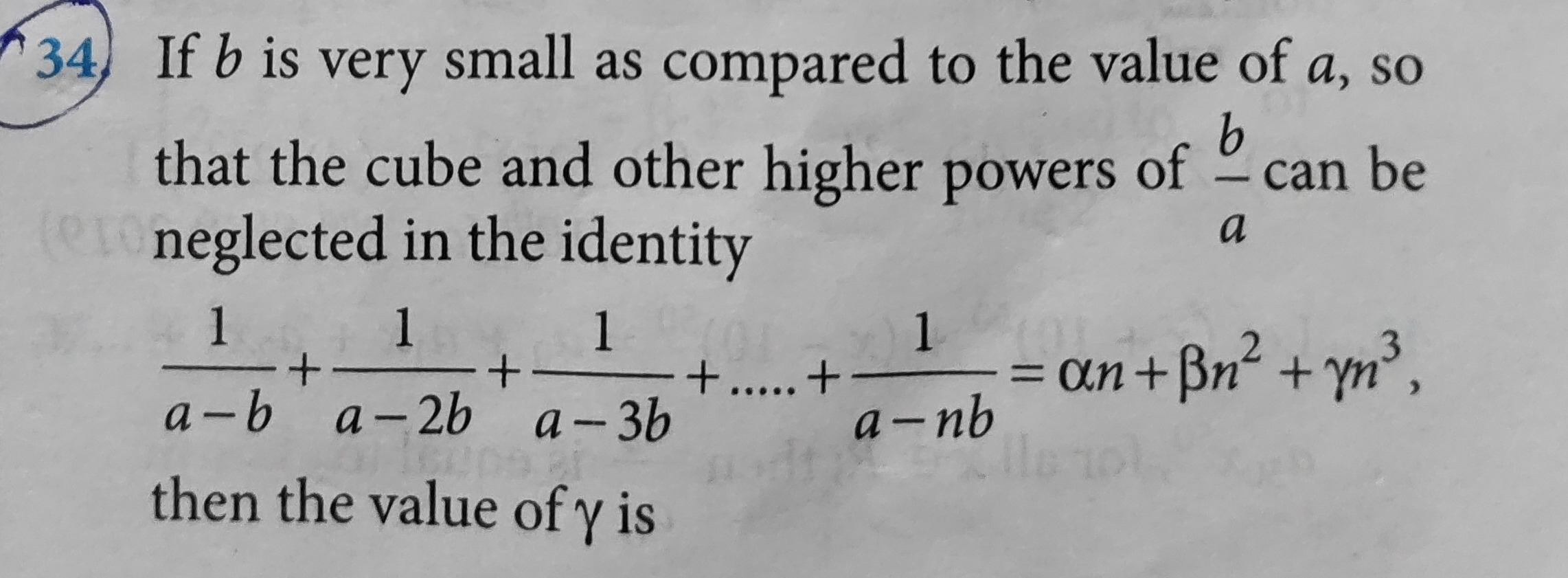
3a3b2
2a3b2
a3b
a3b3
3a3b2
Solution
The general term a−kb1 is expanded using binomial approximation: a−kb1=a(1−akb)1=a1(1−akb)−1 Given that b is very small compared to a, we neglect higher powers of ab. Using the binomial expansion (1−x)−1≈1+x+x2 for small x: (1−akb)−1≈1+akb+(akb)2=1+akb+a2k2b2 So, the general term is approximated as: a−kb1≈a1(1+akb+a2k2b2)=a1+a2kb+a3k2b2 Now, we sum this approximation from k=1 to n: ∑k=1na−kb1≈∑k=1n(a1+a2kb+a3k2b2) =a1∑k=1n1+a2b∑k=1nk+a3b2∑k=1nk2 Using the standard summation formulas: ∑k=1n1=n ∑k=1nk=2n(n+1) ∑k=1nk2=6n(n+1)(2n+1) Substituting these into the sum: Sum≈a1(n)+a2b(2n(n+1))+a3b2(6n(n+1)(2n+1)) We are given the identity αn+βn2+γn3. We need to find the coefficient of n3. Let's expand the sum of squares term: 6n(n+1)(2n+1)=6n(2n2+3n+1)=62n3+3n2+n=31n3+21n2+61n So the third term of the sum is: a3b2(31n3+21n2+61n)=3a3b2n3+2a3b2n2+6a3b2n The full sum, when expanded and collected by powers of n, will have the form: Sum≈(3a3b2)n3+(2a2b+2a3b2)n2+(a1+2a2b+6a3b2)n Comparing this to αn+βn2+γn3, the coefficient of n3 is γ. Therefore, γ=3a3b2.
