Question
Question: If $x = 2 \cos \theta - \cos 2\theta$ and $y = 2 \sin \theta - \sin 2\theta$, then $\frac{d^2y}{dx^2...
If x=2cosθ−cos2θ and y=2sinθ−sin2θ, then dx2d2y is equal to
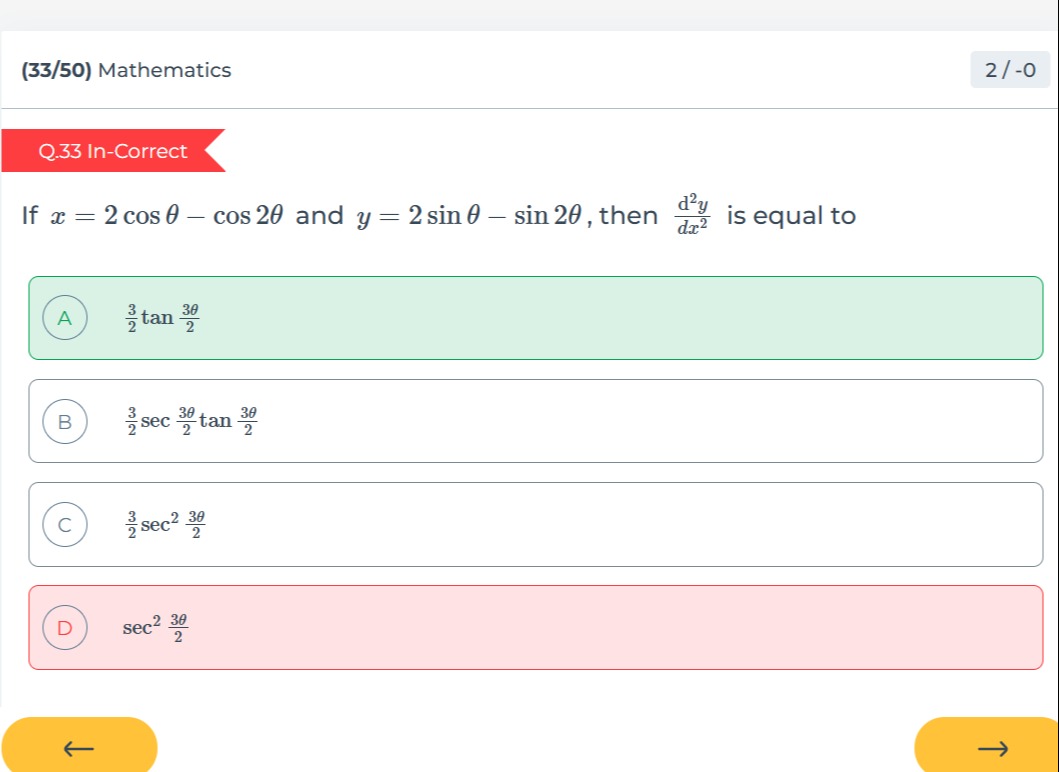
23tan23θ
23sec23θtan23θ
23sec223θ
sec223θ
23sec223θ
Solution
We shall show that by writing the given equations in “sum‐to‐product” form one eventually obtains
dxdy=tan23θ.Differentiating with respect to θ (using the chain‐rule!) gives
dθd(tan23θ)=23sec223θ.Then using the standard formula
dx2d2y=dx/dθdθd(dxdy),one shows (after a little algebra using the identities below) that this simplifies to
dx2d2y=23sec223θ.A short outline of the solution is as follows:
:::mermaid flowchart TD A[Start with x=2cosθ−cos2θ,y=2sinθ−sin2θ] B[Differentiate: dx/dθ=−2sinθ+2sin2θ, dy/dθ=2cosθ−2cos2θ] C[Write numerator and denominator in sum‐to‐product form:] D[cosθ−cos2θ=2sin23θsin2θ] E[sin2θ−sinθ=2cos23θsin2θ] F[Thus, dxdy=2cos23θsin2θ2sin23θsin2θ=tan23θ] G[Differentiate: dθdtan23θ=23sec223θ] H[Divide by dx/dθ (which, after a similar rewriting, cancels the extra factors) to get:] I[dx2d2y=23sec223θ]
A-->B-->C
C-->D
C-->E
D-->F
E-->F
F-->G
G-->H
H-->I
:::
Thus the answer is
23sec223θwhich corresponds to option (C).
Explanation (minimal):
-
Write x and y in forms that allow the use of sum‐to‐product identities: cosθ−cos2θ=2sin23θsin2θ and sin2θ−sinθ=2cos23θsin2θ.
-
Hence, dxdy=2cos23θsin2θ2sin23θsin2θ=tan23θ.
-
Differentiating, dθdtan23θ=23sec223θ.
-
Then using dx2d2y=dx/dθd/dθ(dy/dx) (and the similar rewriting of dx/dθ) one obtains dx2d2y=23sec223θ.
