Solveeit Logo
Login

Question

Question: $I = \int e^{(x\sin x+\cos x)} \left( \frac{x^4 \cos^3 x - x \sin x + \cos x}{x^2 \cos^2 x} \right)...

I=∫e(xsin⁡x+cos⁡x)(x4cos⁡3x−xsin⁡x+cos⁡xx2cos⁡2x)dxI = \int e^{(x\sin x+\cos x)} \left( \frac{x^4 \cos^3 x - x \sin x + \cos x}{x^2 \cos^2 x} \right) dx, then I equals -

A

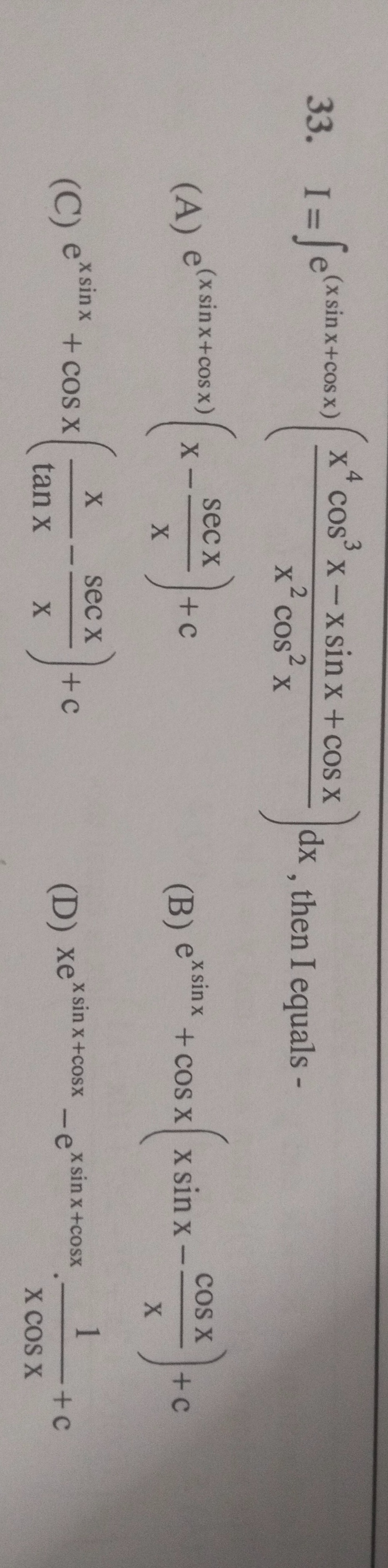
e(xsin⁡x+cos⁡x)(x−sec⁡xx)+ce^{(x\sin x+\cos x)} \left( x - \frac{\sec x}{x} \right) + c

B

exsin⁡x+cos⁡x(xsin⁡x−cos⁡xx)+ce^{x\sin x + \cos x} \left( x \sin x - \frac{\cos x}{x} \right) + c

C

exsin⁡x+cos⁡x(xtan⁡x−sec⁡xx)+ce^{x\sin x + \cos x} \left( \frac{x}{\tan x} - \frac{\sec x}{x} \right) + c

D

xexsin⁡x−cos⁡x−exsin⁡x+cos⁡x⋅1xcos⁡x+cxe^{x\sin x - \cos x} - e^{x\sin x + \cos x} \cdot \frac{1}{x \cos x} + c

Answer

A

Explanation

Solution

The integral to be evaluated is I=∫e(xsin⁡x+cos⁡x)(x4cos⁡3x−xsin⁡x+cos⁡xx2cos⁡2x)dxI = \int e^{(x\sin x+\cos x)} \left( \frac{x^4 \cos^3 x - x \sin x + \cos x}{x^2 \cos^2 x} \right) dx.

This integral is of the form ∫eg(x)[f(x)g′(x)+f′(x)]dx=eg(x)f(x)+C\int e^{g(x)} [f(x)g'(x) + f'(x)] dx = e^{g(x)} f(x) + C.

First, let's identify g(x)g(x) and g′(x)g'(x):
Let g(x)=xsin⁡x+cos⁡xg(x) = x\sin x + \cos x.
Then, g′(x)=ddx(xsin⁡x+cos⁡x)=(1⋅sin⁡x+xcos⁡x)−sin⁡x=xcos⁡xg'(x) = \frac{d}{dx}(x\sin x + \cos x) = (1 \cdot \sin x + x \cos x) - \sin x = x \cos x.

Next, let's simplify the expression inside the parenthesis:
x4cos⁡3x−xsin⁡x+cos⁡xx2cos⁡2x\frac{x^4 \cos^3 x - x \sin x + \cos x}{x^2 \cos^2 x}
We can split the fraction into individual terms:
=x4cos⁡3xx2cos⁡2x−xsin⁡xx2cos⁡2x+cos⁡xx2cos⁡2x= \frac{x^4 \cos^3 x}{x^2 \cos^2 x} - \frac{x \sin x}{x^2 \cos^2 x} + \frac{\cos x}{x^2 \cos^2 x}
=x2cos⁡x−sin⁡xxcos⁡2x+1x2cos⁡x= x^2 \cos x - \frac{\sin x}{x \cos^2 x} + \frac{1}{x^2 \cos x}

Now, we need to find an f(x)f(x) such that f(x)g′(x)+f′(x)f(x)g'(x) + f'(x) equals the simplified expression above. Let's test the options.

Consider Option (A): e(xsin⁡x+cos⁡x)(x−sec⁡xx)+ce^{(x\sin x+\cos x)} \left( x - \frac{\sec x}{x} \right) + c.
Here, f(x)=x−sec⁡xxf(x) = x - \frac{\sec x}{x}.

Let's calculate f(x)g′(x)f(x)g'(x):
f(x)g′(x)=(x−sec⁡xx)(xcos⁡x)f(x)g'(x) = \left( x - \frac{\sec x}{x} \right) (x \cos x)
=x(xcos⁡x)−sec⁡xx(xcos⁡x)= x(x \cos x) - \frac{\sec x}{x} (x \cos x)
=x2cos⁡x−sec⁡xcos⁡x= x^2 \cos x - \sec x \cos x
Since sec⁡x=1cos⁡x\sec x = \frac{1}{\cos x}, we have sec⁡xcos⁡x=1\sec x \cos x = 1.
So, f(x)g′(x)=x2cos⁡x−1f(x)g'(x) = x^2 \cos x - 1.

Now, let's calculate f′(x)f'(x):
f′(x)=ddx(x−sec⁡xx)f'(x) = \frac{d}{dx} \left( x - \frac{\sec x}{x} \right)
f′(x)=ddx(x)−ddx(sec⁡xx)f'(x) = \frac{d}{dx}(x) - \frac{d}{dx}\left(\frac{\sec x}{x}\right)
Using the quotient rule for sec⁡xx\frac{\sec x}{x}: ddx(uv)=u′v−uv′v2\frac{d}{dx}\left(\frac{u}{v}\right) = \frac{u'v - uv'}{v^2}, where u=sec⁡xu = \sec x and v=xv = x.
u′=sec⁡xtan⁡xu' = \sec x \tan x, v′=1v' = 1.
ddx(sec⁡xx)=(sec⁡xtan⁡x)x−(sec⁡x)(1)x2=xsec⁡xtan⁡x−sec⁡xx2\frac{d}{dx}\left(\frac{\sec x}{x}\right) = \frac{(\sec x \tan x)x - (\sec x)(1)}{x^2} = \frac{x \sec x \tan x - \sec x}{x^2}.
So, f′(x)=1−xsec⁡xtan⁡x−sec⁡xx2f'(x) = 1 - \frac{x \sec x \tan x - \sec x}{x^2}.

Now, let's sum f(x)g′(x)+f′(x)f(x)g'(x) + f'(x):
f(x)g′(x)+f′(x)=(x2cos⁡x−1)+(1−xsec⁡xtan⁡x−sec⁡xx2)f(x)g'(x) + f'(x) = (x^2 \cos x - 1) + \left( 1 - \frac{x \sec x \tan x - \sec x}{x^2} \right)
=x2cos⁡x−xsec⁡xtan⁡x−sec⁡xx2= x^2 \cos x - \frac{x \sec x \tan x - \sec x}{x^2}
To compare this with the integrand, let's express sec⁡x\sec x and tan⁡x\tan x in terms of sin⁡x\sin x and cos⁡x\cos x:
sec⁡x=1cos⁡x\sec x = \frac{1}{\cos x} and tan⁡x=sin⁡xcos⁡x\tan x = \frac{\sin x}{\cos x}.
So, xsec⁡xtan⁡x−sec⁡xx2=x1cos⁡xsin⁡xcos⁡x−1cos⁡xx2\frac{x \sec x \tan x - \sec x}{x^2} = \frac{x \frac{1}{\cos x} \frac{\sin x}{\cos x} - \frac{1}{\cos x}}{x^2}
=xsin⁡xcos⁡2x−1cos⁡xx2= \frac{\frac{x \sin x}{\cos^2 x} - \frac{1}{\cos x}}{x^2}
=xsin⁡x−cos⁡xcos⁡2xx2= \frac{\frac{x \sin x - \cos x}{\cos^2 x}}{x^2}
=xsin⁡x−cos⁡xx2cos⁡2x= \frac{x \sin x - \cos x}{x^2 \cos^2 x}.

Substitute this back into the sum:
f(x)g′(x)+f′(x)=x2cos⁡x−(xsin⁡x−cos⁡xx2cos⁡2x)f(x)g'(x) + f'(x) = x^2 \cos x - \left( \frac{x \sin x - \cos x}{x^2 \cos^2 x} \right)
=x2cos⁡x−xsin⁡xx2cos⁡2x+cos⁡xx2cos⁡2x= x^2 \cos x - \frac{x \sin x}{x^2 \cos^2 x} + \frac{\cos x}{x^2 \cos^2 x}
=x2cos⁡x−sin⁡xxcos⁡2x+1x2cos⁡x= x^2 \cos x - \frac{\sin x}{x \cos^2 x} + \frac{1}{x^2 \cos x}.

This expression exactly matches the simplified integrand.
Therefore, the integral I=eg(x)f(x)+C=e(xsin⁡x+cos⁡x)(x−sec⁡xx)+cI = e^{g(x)} f(x) + C = e^{(x\sin x+\cos x)} \left( x - \frac{\sec x}{x} \right) + c.