Question

A slender homogeneous rod of length 2L floats partly immersed in water, being supported by a string fastened to one of its ends, as shown. The specific gravity of the rod is 0.75. The length of rod that extends out of water is:

• A. L
• B. $\frac{1}{2}$L
• C. $\frac{1}{4}$L
• D. 3 L

Answer 1

Answer: (A)

L

Answer 2

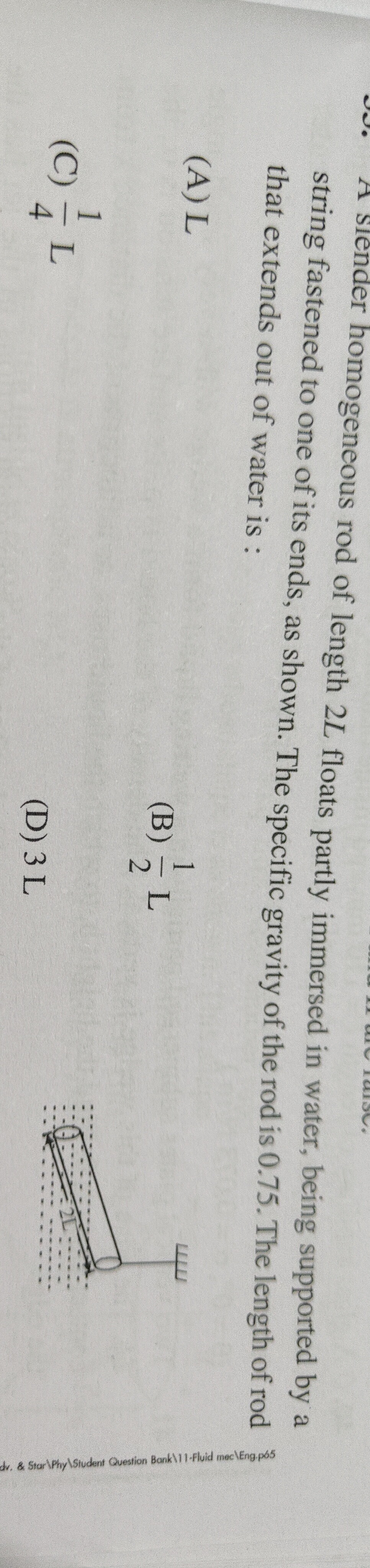
Let $S$ be the specific gravity of the rod, $S = 0.75$. Let $\rho_r$ be the density of the rod and $\rho_w$ be the density of water. Then $\rho_r = S \rho_w = 0.75 \rho_w$. The total length of the rod is $2L$. Let $A$ be the cross-sectional area. The weight of the rod is $W = \rho_r (2LA) g = 0.75 \rho_w (2LA) g = 1.5 \rho_w L A g$. Let $h$ be the length of the rod immersed in water. The buoyant force is $F_B = \rho_w (hA) g$. The rod is supported by a string, so the equilibrium equation is $F_B + T = W$, where $T$ is the tension in the string. Substituting the expressions for $F_B$ and $W$: $\rho_w h A g + T = 1.5 \rho_w L A g$. Since $T \ge 0$, we have $\rho_w h A g \le 1.5 \rho_w L A g$, which implies $h \le 1.5L$. The length of the rod that extends out of water is $l_{out} = 2L - h$. Since $h \le 1.5L$, $l_{out} = 2L - h \ge 2L - 1.5L = 0.5L$. If $l_{out} = L$, then $h = 2L - L = L$. In this case, $F_B = \rho_w (LA) g$. The equilibrium equation becomes $\rho_w LA g + T = 1.5 \rho_w LA g$, so $T = 0.5 \rho_w LA g$. Since $T > 0$, this is a valid scenario. If $l_{out} = \frac{1}{2}L$, then $h = 2L - \frac{1}{2}L = 1.5L$. In this case, $F_B = \rho_w (1.5LA) g = 1.5 \rho_w LA g$. So $F_B = W$, which means $T=0$. This implies the string is slack and not supporting the rod, contradicting the problem statement. If $l_{out} = \frac{1}{4}L$, then $h = 2L - \frac{1}{4}L = \frac{7}{4}L = 1.75L$. Then $F_B = \rho_w (1.75LA) g$. The equilibrium equation would be $1.75 \rho_w LA g + T = 1.5 \rho_w LA g$, which gives $T = -0.25 \rho_w LA g$. Tension cannot be negative, so this is impossible. The option $3L$ is impossible as the total length is $2L$. Therefore, the only valid option is $L$.