Question

A body is projected up a smooth inclined plane with velocity V from the point A as shown in the figure. The angle of inclination is 45° and the top is connected to a well of diameter 40 m. If the body just manages to cross the well, what is the value of V ? (Length of inclined plane is $20\sqrt{2}$ m):-

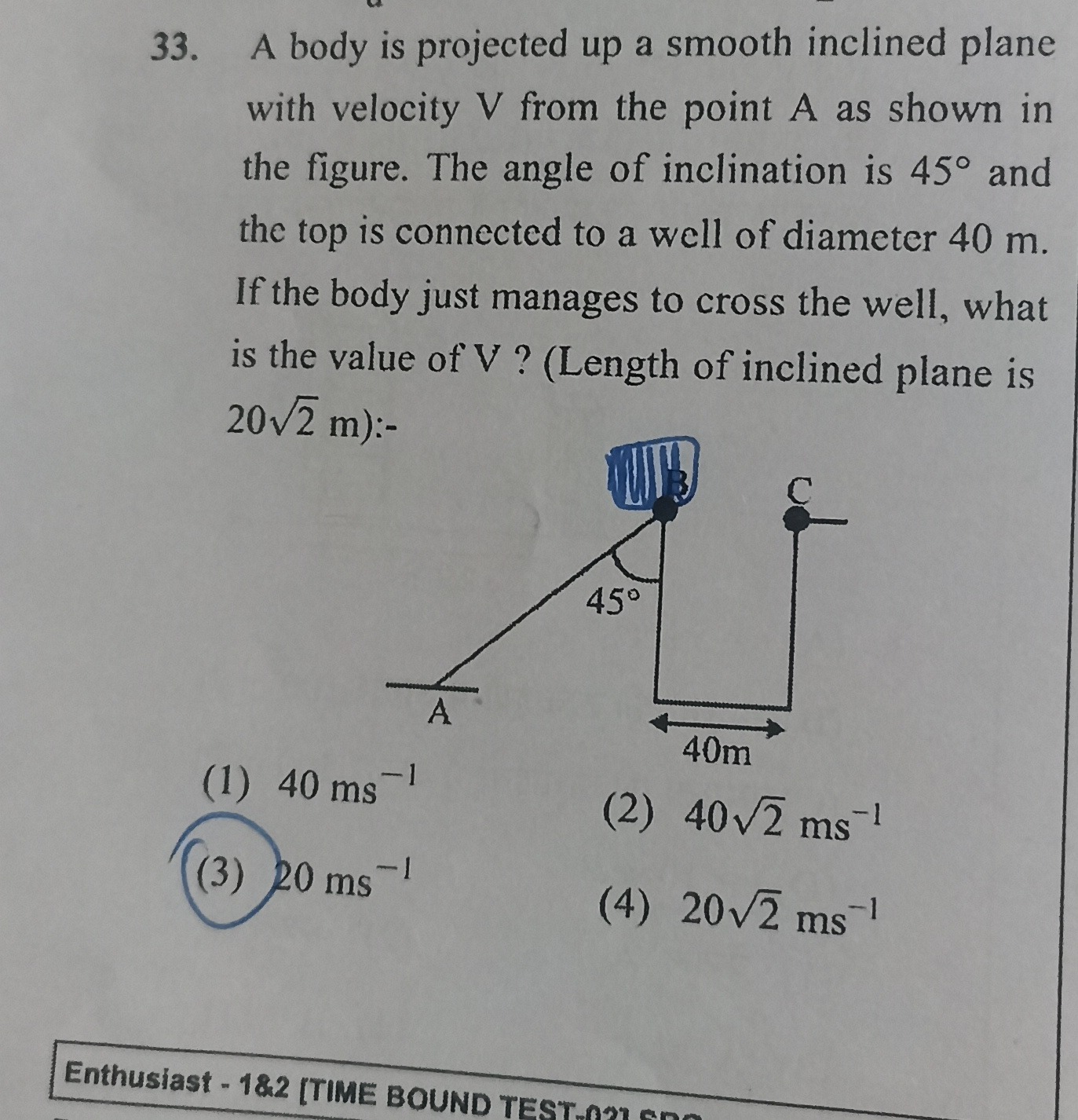
• A. 40 $ms^{-1}$
• B. $40\sqrt{2}$ $ms^{-1}$
• C. 20 $ms^{-1}$
• D. $20\sqrt{2}$ $ms^{-1}$

Answer 1

Answer: (D)

$20\sqrt{2}$ $ms^{-1}$

Answer 2

The acceleration up the incline is $a = -g\sin\theta = -g/\sqrt{2}$. The velocity at the top of the incline ($v_B$) is found using $v_B^2 = V^2 + 2aL = V^2 + 2(-g/\sqrt{2})(20\sqrt{2}) = V^2 - 40g$.

For projectile motion, the range $R = 40$ m. Using the range formula $R = \frac{v_B^2 \sin(2\alpha)}{g}$, with $\alpha = 45^\circ$, we get $40 = \frac{v_B^2 \sin(90^\circ)}{g} = \frac{v_B^2}{g}$, so $v_B^2 = 40g$.

Equating the expressions for $v_B^2$: $V^2 - 40g = 40g \implies V^2 = 80g$. With $g = 10 \, m/s^2$, $V^2 = 800$, so $V = \sqrt{800} = 20\sqrt{2} \, m/s$.