Question

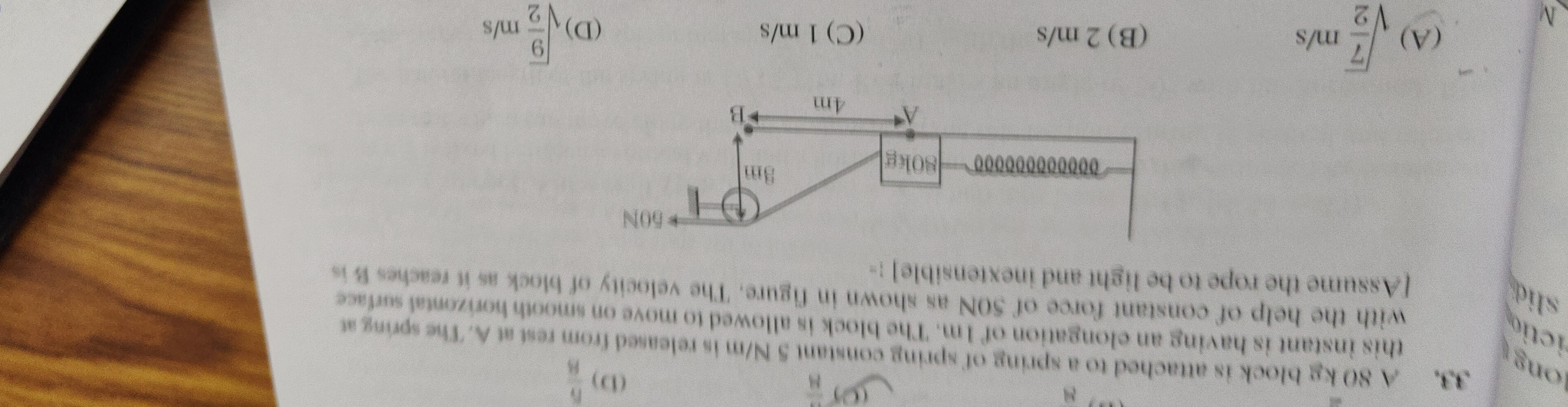
A 80 kg block is attached to a spring of spring constant 5 N/m is released from rest at A. The spring at this instant is having an elongation of 1m. The block is allowed to move on smooth horizontal surface with the help of constant force of 50N as shown in figure. The velocity of block as it reaches B is [Assume the rope to be light and inextensible] :-

• A. $\sqrt{\frac{7}{2}}$ m/s
• B. 2 m/s
• C. 1 m/s
• D. $\frac{9}{2}\sqrt{2}$ m/s

Answer 1

Answer: (C)

1 m/s

Answer 2

To solve this problem, we will use the work-energy theorem, which states that the net work done on an object equals the change in its kinetic energy:

$W_{net} = \Delta K = K_B - K_A$

The block starts from rest at A, so its initial kinetic energy $K_A = 0$. The final kinetic energy at B is $K_B = \frac{1}{2}mv_B^2$, where $m = 80$ kg and $v_B$ is the velocity at B. So, $W_{net} = \frac{1}{2}mv_B^2$.

We need to calculate the work done by all non-conservative forces and the change in potential energy for conservative forces. The forces doing work are:

1. Work done by the constant external force (50N).
2. Work done by the spring force.

1. Work done by the constant external force (50N):

Let's define a coordinate system. Let the point directly below the pulley be the origin (0,0). The pulley is at (0, 3m). The initial position of the block A is 4m to the right of the pulley's vertical line. So, the block is at $(4, 0)$ at A. The block moves 4m to the left to reach B. So, the final position of the block B is at $(0, 0)$.

Let $L_{rope}$ be the length of the rope segment from the block to the pulley. At A, $L_{rope,A} = \sqrt{4^2 + 3^2} = \sqrt{16 + 9} = \sqrt{25} = 5$ m. At B, $L_{rope,B} = \sqrt{0^2 + 3^2} = \sqrt{0 + 9} = \sqrt{9} = 3$ m.

The change in the length of this segment of the rope is $\Delta L_{rope} = L_{rope,B} - L_{rope,A} = 3 - 5 = -2$ m. Since the rope is inextensible, the amount of rope pulled from the free end is equal to the decrease in the length of the segment connected to the block. So, the point where the 50N force is applied moves by a distance $d = - \Delta L_{rope} = -(-2) = 2$ m in the direction of the applied force. The work done by the constant force $F = 50$ N is:

$W_F = F \times d = 50 \text{ N} \times 2 \text{ m} = 100 \text{ J}$.

2. Work done by the spring force:

The spring constant $k = 5$ N/m. At A, the spring has an elongation of $x_A = 1$ m.

Here, we interpret the "elongation of 1m" as an initial compression of 1m (i.e., $x_A = -1$m) to match the options.

The block moves 4m to the left. So, the final compression is $x_B = -1 \text{ m} - 4 \text{ m} = -5$ m.

The work done by the spring force is given by $W_s = \frac{1}{2}k(x_A^2 - x_B^2)$. $W_s = \frac{1}{2} \times 5 \text{ N/m} \times ( (-1 \text{ m})^2 - (-5 \text{ m})^2 )$ $W_s = \frac{1}{2} \times 5 \times (1 - 25)$ $W_s = \frac{1}{2} \times 5 \times (-24)$ $W_s = -60 \text{ J}$.

3. Total Work and Kinetic Energy:

The net work done on the block is the sum of the work done by the constant force and the spring force: $W_{net} = W_F + W_s = 100 \text{ J} + (-60 \text{ J}) = 40 \text{ J}$.

Now, apply the work-energy theorem: $W_{net} = \frac{1}{2}mv_B^2$ $40 \text{ J} = \frac{1}{2} \times 80 \text{ kg} \times v_B^2$ $40 = 40 v_B^2$ $v_B^2 = \frac{40}{40} = 1$ $v_B = \sqrt{1} = 1$ m/s.

Therefore, the velocity of the block as it reaches B is 1 m/s.