Question

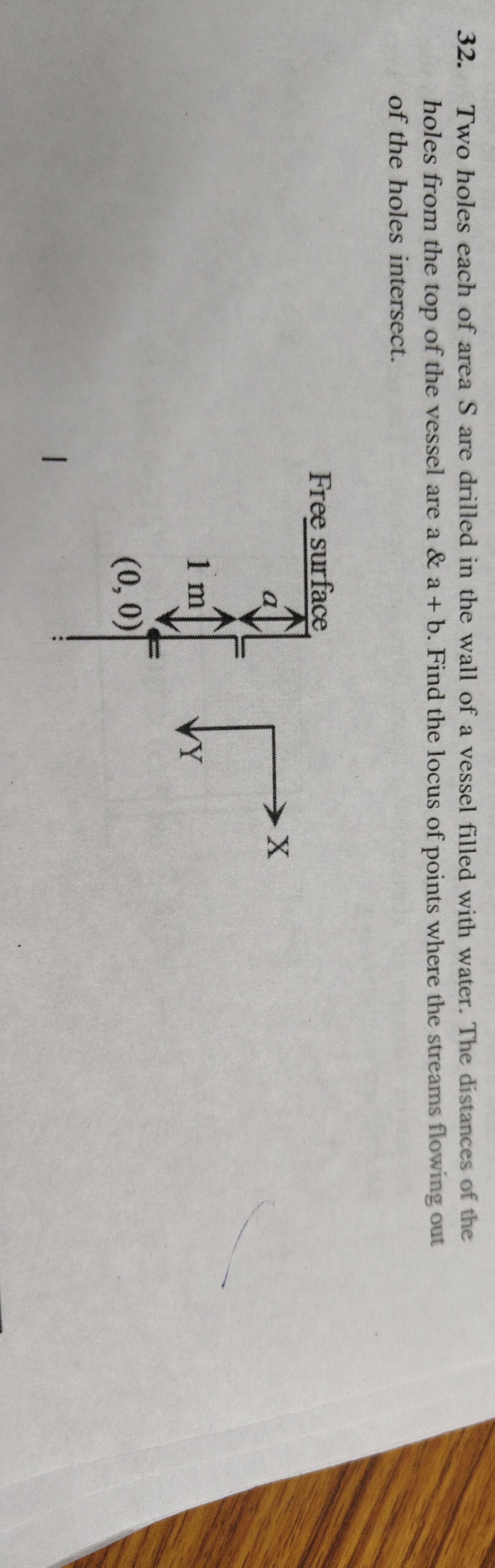
Two holes each of area S are drilled in the wall of a vessel filled with water. The distances of the holes from the top of the vessel are a & a + b. Find the locus of points where the streams flowing out of the holes intersect.

• A. x^2 = 4y
• B. y^2 = 4x
• C. x = 4y
• D. y = 4x

Answer 1

Answer: (A)

x^2 = 4y

Answer 2

Let the origin (0,0) be at the level of the first hole, with the y-axis pointing downwards and the x-axis pointing horizontally outwards. The depths of the holes are $h_1 = a$ and $h_2 = a+b$. From the figure, $a=1$ m. The velocity of efflux from the first hole is $v_1 = \sqrt{2gh_1} = \sqrt{2g}$. The trajectory of the first stream is $y = \frac{gx^2}{2v_1^2} = \frac{gx^2}{2(2g)} = \frac{x^2}{4}$.

The velocity of efflux from the second hole is $v_2 = \sqrt{2gh_2} = \sqrt{2g(1+b)}$. The second hole is at a vertical distance $b$ below the first hole, so its coordinates are $(0, b)$. The trajectory of the second stream is $y = b + \frac{gx^2}{2v_2^2} = b + \frac{gx^2}{2(2g(1+b))} = b + \frac{x^2}{4(1+b)}$.

Equating the y-coordinates to find intersection points: $\frac{x^2}{4} = b + \frac{x^2}{4(1+b)}$ $x^2 \left( \frac{1}{4} - \frac{1}{4(1+b)} \right) = b$ $x^2 \left( \frac{1+b-1}{4(1+b)} \right) = b$ $x^2 \left( \frac{b}{4(1+b)} \right) = b$ Assuming $b \neq 0$, $x^2 = 4(1+b)$. The corresponding y-coordinate is $y = \frac{x^2}{4} = \frac{4(1+b)}{4} = 1+b$. Thus, $x^2 = 4y$. This is the locus of intersection points.