Question

Two holes each of area S are drilled in the wall of a vessel filled with water. The distances of the holes from the top of the vessel are a & a + b. Find the locus of points where the streams flowing out of the holes intersect.

Answer 1

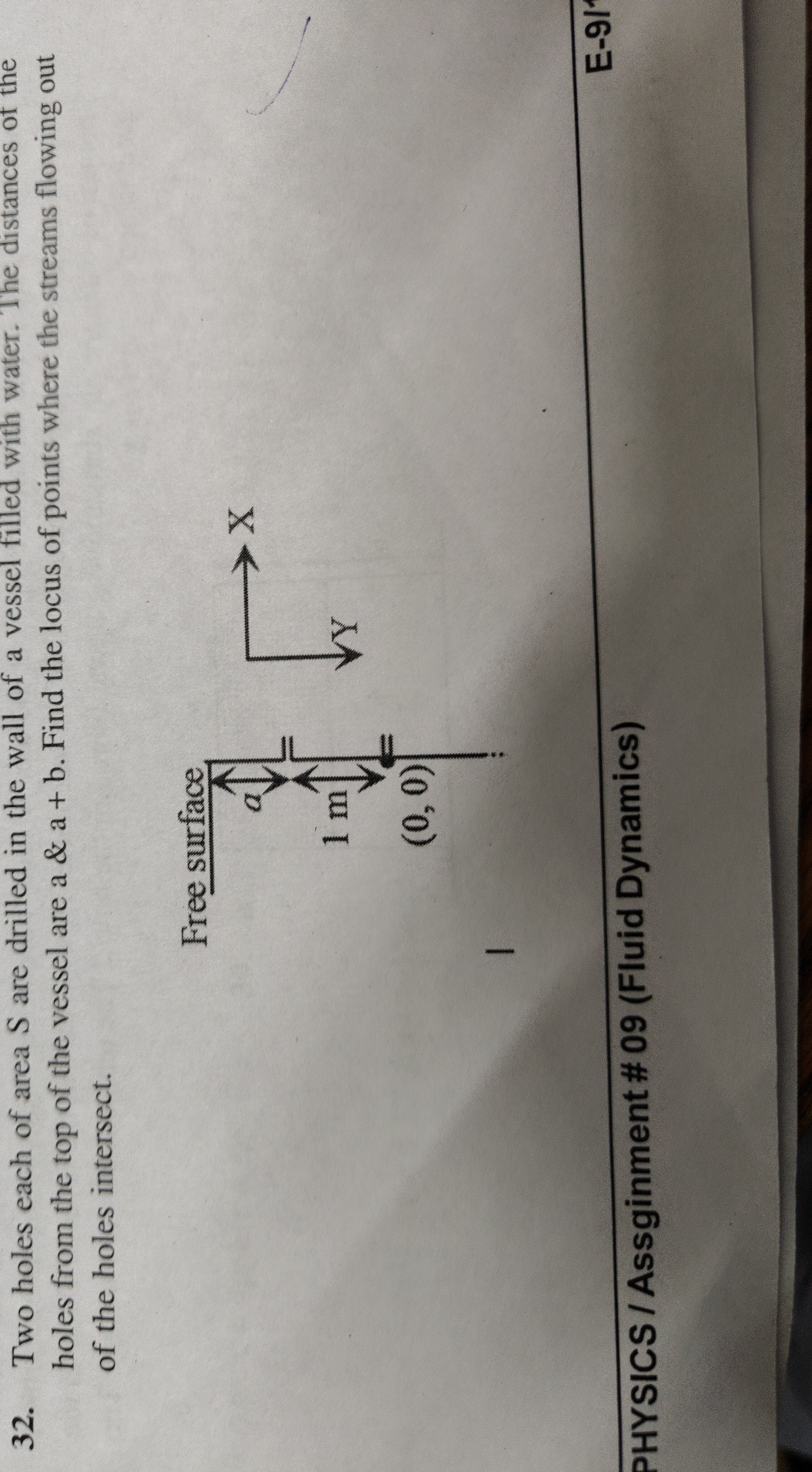
The locus of points where the streams flowing out of the holes intersect is given by the equation $y^2 - x^2 = b^2$.

Answer 2

The trajectory of a water stream from a hole at depth $h$ is given by $y = h + \frac{x^2}{4h}$, where $y$ is the vertical distance from the free surface and $x$ is the horizontal distance from the wall. For two holes at depths $h_1$ and $h_2$, the intersection point $(x,y)$ satisfies $y = h_1 + \frac{x^2}{4h_1}$ and $y = h_2 + \frac{x^2}{4h_2}$. Solving these equations yields $x^2 = 4h_1 h_2$ and $y = h_1+h_2$. Thus, $y^2 - x^2 = (h_1+h_2)^2 - 4h_1h_2 = (h_1-h_2)^2$. Given depths are $a$ and $a+b$, so the difference in depths is $b$. Therefore, the locus is $y^2 - x^2 = b^2$.