Question
Question: The integral $\int (\frac{x}{x \sin x + \cos x})^2 dx$ is equal to: (2020) (where C is a constant o...
The integral ∫(xsinx+cosxx)2dx is equal to: (2020)
(where C is a constant of integration):
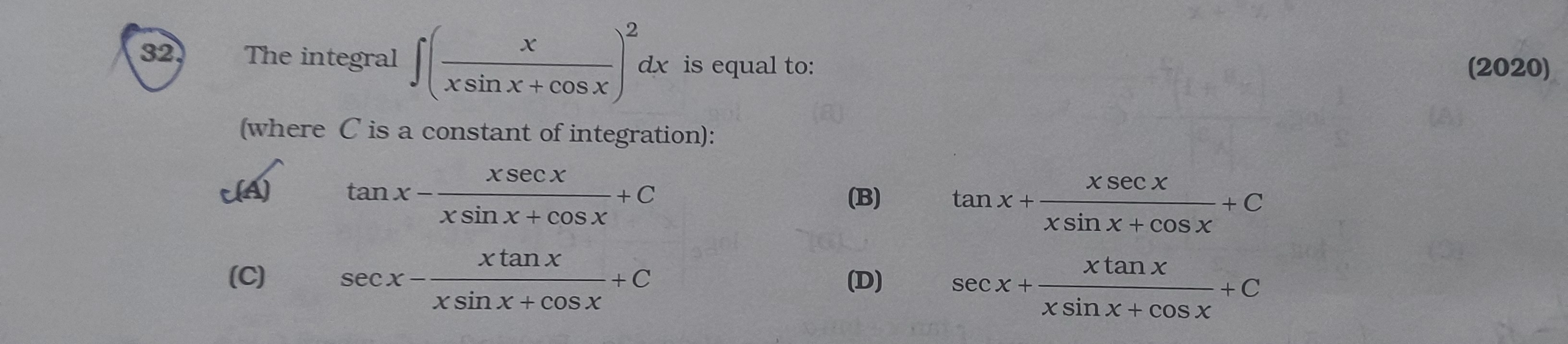
tanx−xsinx+cosxxsecx+C
tanx+xsinx+cosxxsecx+C
secx−xsinx+cosxxtanx+C
secx+xsinx+cosxxtanx+C
tanx−xsinx+cosxxsecx+C
Solution
To evaluate the integral I=∫(xsinx+cosxx)2dx, we can use the method of integration by parts.
Let's denote the expression in the denominator as f(x)=xsinx+cosx. First, find the derivative of f(x): f′(x)=dxd(xsinx+cosx) Using the product rule for xsinx: dxd(xsinx)=1⋅sinx+x⋅cosx. Using the derivative for cosx: dxd(cosx)=−sinx. So, f′(x)=(sinx+xcosx)−sinx=xcosx.
Now, rewrite the integrand in a form suitable for integration by parts. The integrand is (xsinx+cosx)2x2. We can write this as cosxx⋅(xsinx+cosx)2xcosx. This form suggests choosing: u=cosxx=xsecx dv=(xsinx+cosx)2xcosxdx=(f(x))2f′(x)dx
Now, we find du and v: du=dxd(xsecx)dx=(1⋅secx+x⋅secxtanx)dx=(secx+xsecxtanx)dx. v=∫(f(x))2f′(x)dx. Let t=f(x), then dt=f′(x)dx. So v=∫t21dt=−t1=−xsinx+cosx1.
Apply the integration by parts formula: ∫udv=uv−∫vdu. I=(xsecx)(−xsinx+cosx1)−∫(−xsinx+cosx1)(secx+xsecxtanx)dx I=−xsinx+cosxxsecx+∫xsinx+cosxsecx+xsecxtanxdx
Now, let's evaluate the remaining integral J=∫xsinx+cosxsecx+xsecxtanxdx. Simplify the numerator: secx+xsecxtanx=cosx1+xcosx1cosxsinx =cos2xcosx+cos2xxsinx=cos2xcosx+xsinx
Substitute this back into the integral J: J=∫xsinx+cosxcos2xcosx+xsinxdx Assuming xsinx+cosx=0, we can cancel the term (cosx+xsinx) from the numerator and denominator: J=∫cos2x1dx=∫sec2xdx J=tanx+C′ (where C′ is the constant of integration for J)
Substitute J back into the expression for I: I=−xsinx+cosxxsecx+tanx+C
Rearranging the terms, we get: I=tanx−xsinx+cosxxsecx+C
Comparing this result with the given options, our result matches option (A).
