Question

$\cos x \cdot \cos 7x - \cos 5x \cdot \cos 13x =$

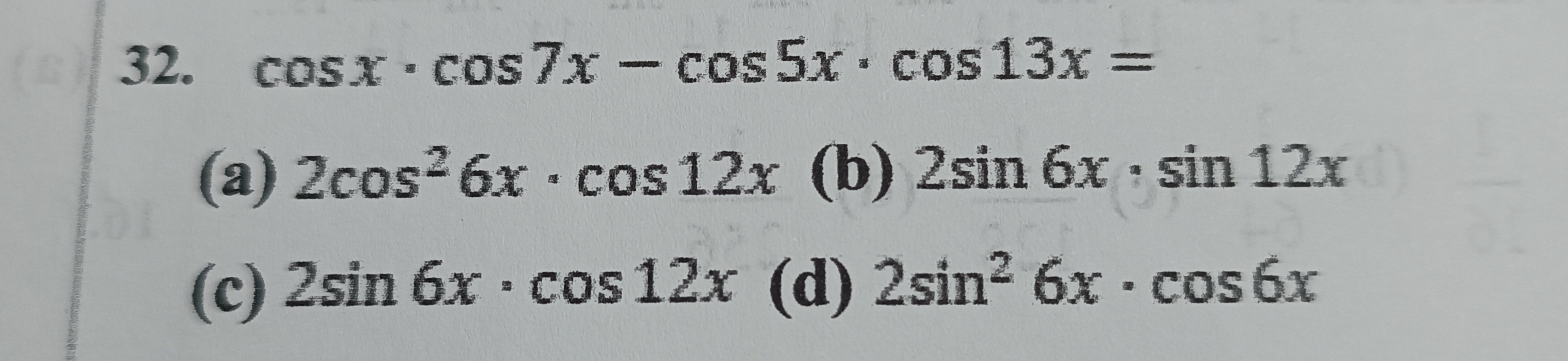
• A. $2\cos^2 6x \cdot \cos 12x$
• B. $2\sin 6x \cdot \sin 12x$
• C. $2\sin 6x \cdot \cos 12x$
• D. $2\sin^2 6x \cdot \cos 6x$

Answer 1

Answer: (B)

(b)

Answer 2

To simplify the expression $\cos x \cdot \cos 7x - \cos 5x \cdot \cos 13x$, we use the product-to-sum trigonometric identity:

$2 \cos A \cos B = \cos(A+B) + \cos(A-B)$

This can be rewritten as $\cos A \cos B = \frac{1}{2} [\cos(A+B) + \cos(A-B)]$.

1. Simplify the first term, $\cos x \cdot \cos 7x$: Let $A=x$ and $B=7x$. $\cos x \cdot \cos 7x = \frac{1}{2} [\cos(x+7x) + \cos(x-7x)] = \frac{1}{2} [\cos(8x) + \cos(-6x)] = \frac{1}{2} [\cos 8x + \cos 6x]$

2. Simplify the second term, $\cos 5x \cdot \cos 13x$: Let $A=5x$ and $B=13x$. $\cos 5x \cdot \cos 13x = \frac{1}{2} [\cos(5x+13x) + \cos(5x-13x)] = \frac{1}{2} [\cos(18x) + \cos(-8x)] = \frac{1}{2} [\cos 18x + \cos 8x]$

3. Substitute these simplified terms back into the original expression: $\cos x \cdot \cos 7x - \cos 5x \cdot \cos 13x = \frac{1}{2} [\cos 8x + \cos 6x] - \frac{1}{2} [\cos 18x + \cos 8x] = \frac{1}{2} [\cos 8x + \cos 6x - \cos 18x - \cos 8x] = \frac{1}{2} [\cos 6x - \cos 18x]$

4. Use the sum-to-product trigonometric identity for $\cos C - \cos D$: The identity is: $\cos C - \cos D = -2 \sin \left(\frac{C+D}{2}\right) \sin \left(\frac{C-D}{2}\right)$. Let $C=6x$ and $D=18x$. $\cos 6x - \cos 18x = -2 \sin \left(\frac{6x+18x}{2}\right) \sin \left(\frac{6x-18x}{2}\right) = -2 \sin (12x) \sin (-6x) = 2 \sin (12x) \sin (6x)$

5. Substitute this result back into the expression from Step 3: $\frac{1}{2} [\cos 6x - \cos 18x] = \frac{1}{2} [2 \sin (12x) \sin (6x)] = \sin (12x) \sin (6x)$

Comparing this result with the given options, we see a discrepancy of a factor of 2. Assuming a typo in the question or options, option (b) is the closest.