Question

An ant is at a corner of a cubical room of side a. The ant can move with a constant speed u. The minimum time taken to reach the farthest corner of the cube is:

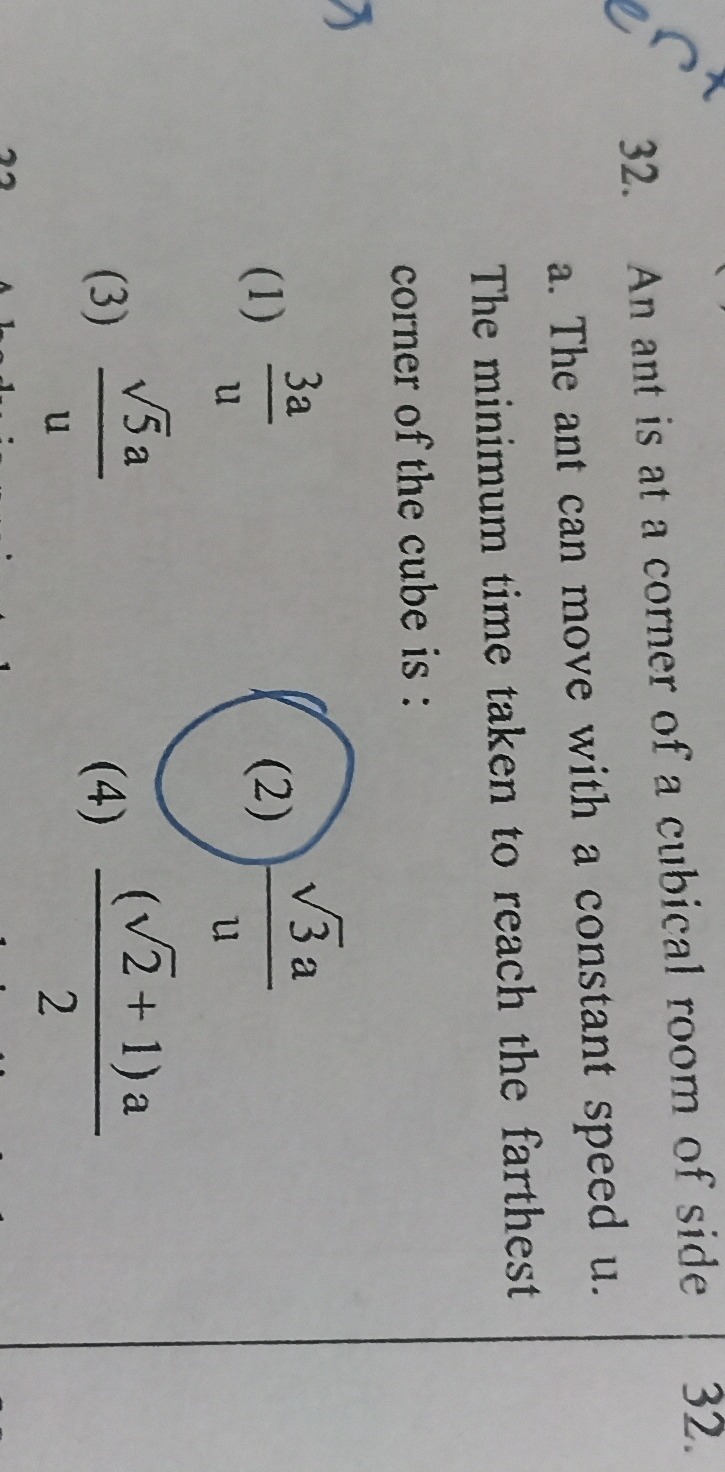
• A. (1) $\frac{3a}{u}$
• B. (2) $\frac{\sqrt{3}a}{u}$
• C. (3) $\frac{\sqrt{5}a}{u}$
• D. (4) $\frac{(\sqrt{2}+1)a}{2}$

Answer 1

Answer: (C)

$\frac{\sqrt{5}a}{u}$

Answer 2

To find the minimum time, we need to find the minimum distance the ant can travel on the surfaces of the cube. This can be visualized by unfolding the cube. Imagine unfolding two adjacent faces of the cube, creating a rectangle with dimensions $a \times 2a$. The starting corner and the farthest corner are at opposite ends of the diagonal of this rectangle. Using the Pythagorean theorem, the distance is $\sqrt{a^2 + (2a)^2} = \sqrt{a^2 + 4a^2} = \sqrt{5a^2} = a\sqrt{5}$. The minimum time is then distance/speed: $\text{Time} = \frac{a\sqrt{5}}{u}$.