Question

Two non-conducting spheres of radii R₁ and R₂ and carrying uniform volume charge densities +$\rho$ and -$\rho$, respectively, are placed such that they partially overlap, as shown in the figure. At all points in the overlapping region:

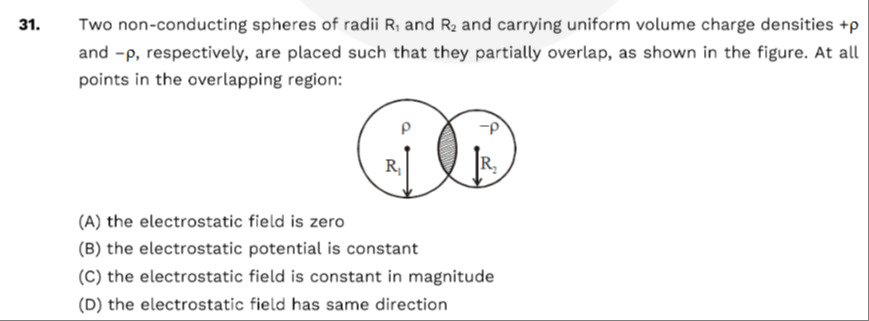
• A. the electrostatic field is zero
• B. the electrostatic potential is constant
• C. the electrostatic field is constant in magnitude
• D. the electrostatic field has same direction

Answer 1

Answer: (C), (D)

C and D

Answer 2

Let the centers of the two spheres be $C_1$ and $C_2$ with separation vector

$\mathbf{d} = \mathbf{C_2} - \mathbf{C_1}$.

For a uniformly charged non-conducting sphere (with volume charge density $\rho$), the electric field at an internal point (at a vector distance $\mathbf{r}$ from its center) is

$\mathbf{E} = \frac{\rho\,\mathbf{r}}{3\varepsilon_0}$.

For a point P in the overlapping region, let $\mathbf{r}_1 = \mathbf{P} - \mathbf{C_1}$ relative to the positive sphere and $\mathbf{r}_2 = \mathbf{P} - \mathbf{C_2}$ relative to the negative sphere. Thus, the net electric field at P is

$\mathbf{E}_P = \frac{\rho\,\mathbf{r}_1}{3\varepsilon_0} - \frac{\rho\,\mathbf{r}_2}{3\varepsilon_0} = \frac{\rho}{3\varepsilon_0}\,(\mathbf{r}_1 - \mathbf{r}_2)$.

Notice that

$\mathbf{r}_1 - \mathbf{r}_2 = (\mathbf{P} - \mathbf{C_1}) - (\mathbf{P} - \mathbf{C_2}) = \mathbf{C_2} - \mathbf{C_1} = \mathbf{d}$,

which is independent of the choice of P in the overlapping region. Thus,

$\mathbf{E}_P = \frac{\rho\,\mathbf{d}}{3\varepsilon_0}$,

a constant vector having both constant magnitude and constant direction throughout the overlapping region.